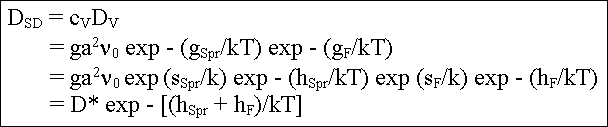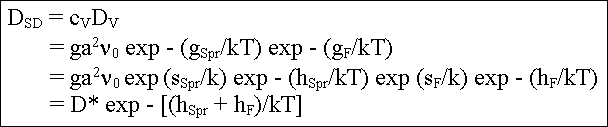3.2.2 Selbstdiffusion

	Die Frage ist , wie sich die Atome schon im Idealfall des perfekten Kristalls bewegen (bei mehratomigen Kristallen für jede Atomsorte getrennt).
	Die Antwort ist am einfachsten für einen simplen (Einfach)leerstellen- Mechanismus in einatomigen (kubischen) Kristallen zu geben. Einsetzen der Gleichungen für die Leerstellen- Konzentration und die Sprungrate für Leerstellen ergibt
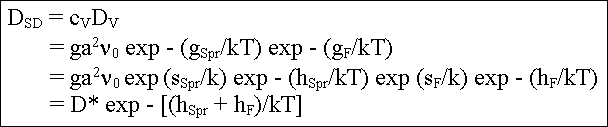
	Dabei ist erwähnenswert:
		ähnlich wie bei der Bildungsentropie, haben wir jetzt auch eine Sprungentropie. Auch sie kommt aus der Änderung der Gitteschwingungen der Atome beim Sprung und liegt in der Größenordnung 1k.
		Als relevanter Parameter tritt die Summe aus Bildungs- und Sprungenthalpie auf.
		Die Vorfaktoren können zu einem D* zusammengezogen werden, der als wesentliche unbekannte Größen die Entropien enthält.
		Eine Arrhenius-Auftragung (ln D über 1/T) ergibt eine Gerade, die Steigung ist durch hSpr+ hF gegeben, der Achsenabschnitt ergibt den Vorfaktor
		Die Selbstdiffusion über (intrinsische) Zwischengitteratome und sieht im Prinzip genauso aus.
	hierzu siehe auch: englisches Skript
	Zahlenwerte für die Selbstdiffusion in Silizium (18kB): 10-21 bis 10-16 m2/s , abhängig von T