 |
Atomare Fehlstellen sind im allgemeinen beweglich (zumindest
bei hohen Temperaturen). Damit werden auch Atome beweglich - wir beobachten das
Phänomen der Festkörperdiffusion, d.h. Materietransport im
Festkörper.
|
 |
Moderne Technologie beruht in vielen
Technologiefeldern auf der Diffusion in Festkörpern. Besonders prominent
sind |
|
 |
Mikroelektronik
und Optoelektronik |
|
 |
Sensorik in vielen Ausführungen |
|
 |
Batterien,
Akkus, Brennstoffzellen,
aber z.B. auch die |
|
 |
Kerntechnik (Diffusion von Neutronen). |
 |
Art und Konzentration der vorhanden atomaren
Fehlstellen, Gleichgewichtsbetrachtungen (globales, lokales
Gleichgewicht, oder totales Nichtgleichgewicht), und atomare Mechanismen
der Diffusion bestimmen das Ergebnis - die mögliche Vielfalt ist sehr
groß, selbst bei einfachsten Systemen (z.B. Phosphor in Silizium).
|
Wiederholung einiger bekannter Beziehungen
|
 |
1. Ficksches Gesetz |
|
 |
Fluß j proportional zum Konzentrationsgradient
|
|
 |
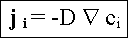 |
|
 |
der Index i bezieht sich dabei auf die Teilchensorte. (Bei der
Frage, ob, und ggf. wie, die Teilchensorte i diffundiert, falls nur die
Sorte k einen Konzentrationsgradienten zeigt, wird es spannend).
Erheblich allgemeiner gilt |
|
 |
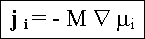
mit m=chem. Potential;
M=Beweglichkeit
Da der Gradient des chemischen Potentials auch bei konst. Konzentration von 0
verschieden sein kann, sind damit auch Phämonene wie die "uphill
diffusion" erfaßt.
|
 |
Kontinuitätsgleichung |
|
 |
Was in einem Volumenelement sich ändert, kommt aus der
Differenz dessen was rein- und was rausläuft - Konsequenz aus dem
Erhaltungssatz der Teilchenzahl. |
|
 |
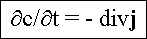 |
|
 |
Stimmt natürlich dann nicht, wenn Teilchen vernichtet
oder erzeugt werden können. |
 |
2. Ficksches Gesetz |
|
 |
Die zeitliche Änderung der Konzentration ist proportional
zur zweiten Ableitung der Konzentration (Aus 1. Fickschem Gesetz +
Kontinuitätsgleichung) |
|
 |
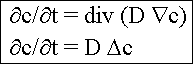 oder für D=konst. oder für D=konst.
|
 |
Lösungen der Fickschen Gesetze sind im
allgemeinen nicht einfach. |
|
 |
Trotz simpler Differentialgleichungen existieren in der Regel
keine simplen Lösungen. |
|
 |
Bereits behandelt: Eindiffusion aus unendlicher oder endlicher
Quelle (Gaußverteilung, Fehlerfunktion; bei ELYMAT mit Quellen und
Senken). |
|
 |
Lösungen für viele behandelte Fälle in
Handbüchern. |
|
 |
Wärmeleitung (in Festkörpern) ist mathematisch
äquivalent, weil letztendlich auch durch Diffusion vermittelt. |
|
 |
Kompliziertere Diffusuionsphänomene sind letzlich nur
dann mit wenigen anpaßbaren Parametern nur zu behandeln, wenn die
atomaren Mechanismen bekannt sind und in die Modelle eingebaut werden. |
|
 |
Die statistischen Funktionen treten auf, weil die Diffusion
letztlich ein rein statistischer Vorgang ist - das Einzelatom weiß nichts
von seiner (Teilchen)- Umgebung und hüpft rein statistisch (solange nicht
Felder direkt Kräfte ausüben).
|
Kopplung Phänomenologie - Einzelereignis
|
|
|
 |
Strom=Differenz Sprünge nach rechts -
Sprünge nach links führt auf 1. Ficksches Gesetz mit
Diffusionskoeffizient (für kub. Symmetrie) |
|
 |
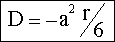 mit a=Gitterkonstante, Faktor 1/6 wg.
kub. Symmetrie. mit a=Gitterkonstante, Faktor 1/6 wg.
kub. Symmetrie.
Wobei die Sprungrate
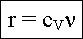
verwendet wird. Dabei ist cV=Konzentration der springenden Spezies
(typischerweise Leerstellen V), und es werden alle Sprünge, nicht nur die
in Flußrichtung, betrachtet [deswegen der Faktor 1/6 bzw g (s.
nächste Formel)] |
|
 |
Mit einem Boltzmann-Ansatz für die Sprungfrequenz v ergibt sich
allgemein
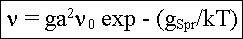
mit g=Geometriefaktor, hSpr=freie Enthalpie für Sprung.
|
 |
"Random Walk" und Diffusion |
|
 |
Korreliert man das bei rein statistischen Sprüngen nach der Zeit
t zurückgelegte mittlere Verschiebungsquadrat (=die
Diffusionlänge2) L2 mit der Diffusionskonstanten, gilt
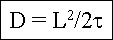
dabei ist t die (mittlere) Lebensdauer, falls das betrachtete Teilchen
"vernichtet" werden kann. |
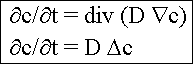 oder für D=konst.
oder für D=konst.