8.3.1 Steps in Interfaces

8.3 Steps in Interfaces

8.3.1 The Relation Between Steps and Dislocations in S = 3 Boundaries

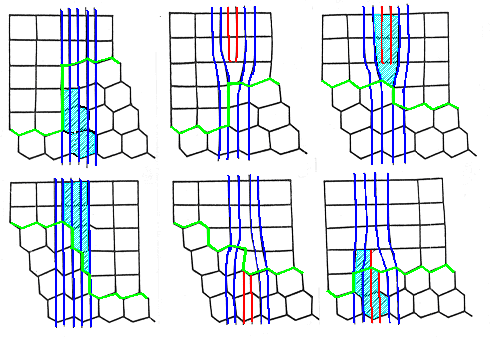
Playing with models of a perfectly fitting phase boundary between a hexagonal and a cubic lattice, one realizes quickly that steps can be incorporated without problems and without dislocations as long as the step height comes in multiples of 3 (in units of the translation vectors of the CSL). This, together with some other cases, is shown below:

steps and dislocations in a phase boundary

The left two pictures show pure steps (or coherent steps). For ease of interpretation, some lattice planes of the DSC lattice are shown in blue; ending lattice planes of the DSC lattice are red. Ending lattice fringes, as seen on a HRTEM micrograph, are indicated in light blue - note that they are not the same thing as lattice planes. The phase boundary itself is shown in light green.

Included in the drawing are also two pure DSC lattice dislocations (middle pictures). They are true dislocations because they can be constructed with the Volterra method as demonstrated before, and they have the 1/r stress field that is a hallmark of dislocations. Sometimes they are called coherency dislocations.

Finally, a mix of pure dislocations and pure steps is shown on the right. It is evident that steps going just one plane up or down must be a mix of pure steps and pure dislocations. The same is true for steps going 4 planes up or down and so on. These dislocations are sometimes called anti-coherency dislocations.

Note that there is no way of having a combination of pure steps and dislocations with step height zero.

An unexpected property emerges: Pure steps (sometimes also called coherent ledges) show ending lattice fringes in a HRTEM micrograph, whereas true dislocations in this case are not associated with ending lattice fringes.

Where does that leave us? Is Franks formula, which after all counted Burger vectors in a circuit not unlike the one shown before, not applicable to non-planar boundaries? Why can we see ending lattice fringes in a TEM picture and there is no dislocation?

Well, ending lattice fringes (again note we call it lattice fringe on purpose) are not lattice planes, and at a grain- or phase boundary all lattice planes of one kind end and some of a new kind start. The fact that some visible fringes appear to be continuous in a "fuzzy" projection of the lattices, has no particular meaning in itself. Of course, one lattice plane ending in one crystal may give rise to a lattice fringe ending on a micrograph, too, and thus signify an edge dislocation, but this must not be generalized.

We may, however, make an important generalization of a different kind: A semi-coherent phase or grain boundary, in general, needs at least two qualitatively different kinds of defects in its interface:

Pure DSC-lattice dislocations (generally associated with an intrinsic step), and

Pure steps (without dislocation character, i.e. without a long range stress field).

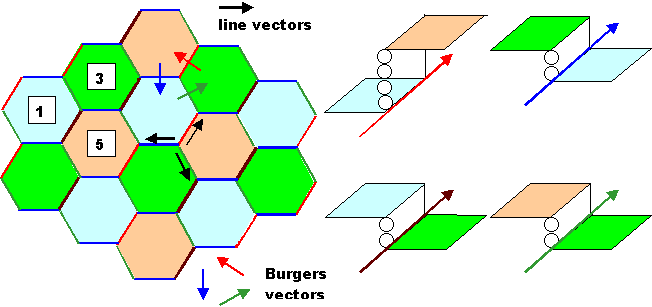
In general both defects are required as we will see if we now compose a (hexagonal) dislocation network in a S = 3 boundary.

Whereas the dislocation network has a perfect threefold rotational symmetry, the boundary is less symmetric. This can be seen when we consider the steps introduced by the dislocations (use the picture above), too:

Steps and dislocations in misfit network

As soon as we defined the line- and Burgers vectors, we realize that the steps associated with pure dislocation are always the same: Looking in the line direction, crossing a pure dislocation would always lead two steps down in this example. If we start a closed circuit at the hexagon labelled "(level) 1" and go across the green dislocation, we end up two atomic planes down on level 3. The same happens if we now cross the blue dislocation; we are down to level 5.

However, in closing the circuit, we must necessarily come up to level 1 again, This is only possible if the dark red dislocations break the symmetry and contain two steps (–2 + 6 = 4). Thus we go two levels down and 6 levels up, which is just right.

This feature, which is clearly a general feature of all boundaries, opens up a whole new can of worms.

There is more than one way to combine pure steps and pure dislocations to create a network that satisfies the requirements for accommodating misfit (this needs the dislocations) and to compensate for the steps introduced by the dislocations (this needs pure steps).

The image of a given boundary in cross-sectional HRTEM can look very different, depending on what kind of possible configuration is cut which way. Lattice fringes may end in several different ways.

The closing failure of a Burgers circuit that counts lattice fringes around a large part of an interface thus cannot be considered as a net count of dislocation Burgers vectors. Combined with a net count of the steps in the interface, however, it may be useful.

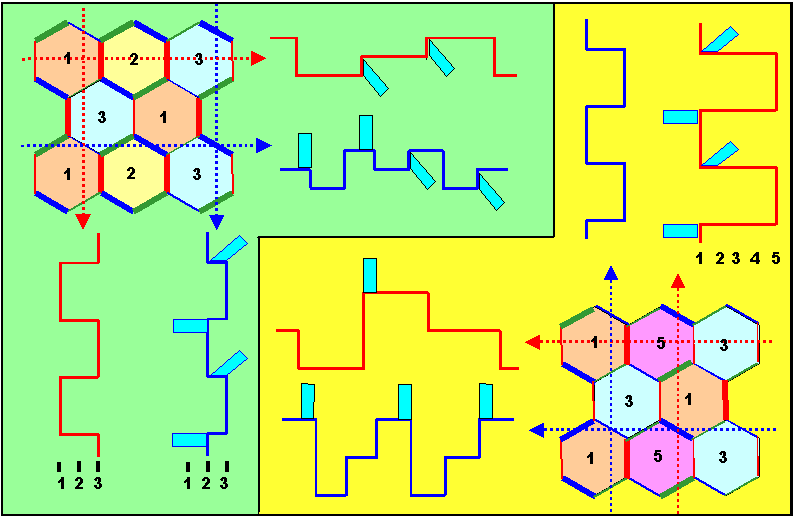
The following graphic illustrates these points

Shown are two possible combinations of dislocations and steps in S = 3 boundaries (of any kind). Dislocations in combination with a coherent step are indicated in bold lines; the numbers in the hexagons indicate the level of the boundary

Two possible geometries are shown in the upper left-hand corner and the lower right-hand corner

Four cross-section through the dislocation/step network are drawn in together with their schematic image in HRTEM. Ending lattice fringes are indicated in light blue (assuming without justification that the image of dislocation/step combinations that are inclined with respect to the electron beam add no further complications).

It becomes clear that the interpretation of an HRTEM image can be a demanding task which will not necessarily give an unambiguous answer. You may try your skills at the picture in the illustration.

But we are still not done with the discussion of the intrinsic geometry of a simple S = 3 boundary. Even if we assume that we have a dislocation/step network of a defined kind (e.g. the one from the upper left-hand corner of the above drawing) and that the boundary is flat apart from the ups and downs of the dislocations, we must expect an added complication:

Since the dislocations/step network most likely formed in small patches and then spreads out, individual patches may be out of "synch", i.e. whenever they meet they will not fit together. This is illustrated below

Dislocations in combination with a coherent step are shown in bold; the color now denotes if the step goes up or down as seen from the inside of the hexagons completely enclosed by "bold" dislocations. The dislocations/step network on the left and right side are identical, but displaced relative to each other by one hexagon.

Along the white line, they obviously don't match. We would need dislocations with a step height of zero, which as we have seen before, do not exist in this geometry.

The only way out is to postulate a new kind of defect, some kind of stacking fault in the dislocation/step lattice. To the best of my knowledge, such a defect has not yet be named or discussed in detail - although it is clearly a necessary feature of general phase- or grain-boundaries.

This serves to illustrate that the last word about structural aspects of defects in crystal has not yet come in. One may ask, of course, if esoterica like the dislocation/step network considerations are of any importance. The answer is: Who knows?

Considering however, that many materials (including natural minerals) are full of phase and grain boundaries, that many properties of theses boundaries are directly linked to their structure and that not much is known about the atomic structure of non-trivial boundaries, it is not totally unrealistic to expect that research will go on.

In the next (and last) subchapter we will briefly look at some more questions in relation to phase boundaries.