Diffusion Coefficient and Atomic Mechanisms

	We are looking for an equation that links the diffusion current j of Ficks 1st law with the individual atomic jumps of a particle like an interstitial atom or a vacancy.
		For simplicities sake we only consider vacancies in a primitive cubic lattice. The extension to interstitials is rather trivial.
		We only consider a one-dimensional geometry.
		Extensions to three dimensions, real crystals and exotic atomic mechanisms, albeit not necessarily easy, do not give new insights and will not be covered.
	Lets look at two lattice planes of a simple cubic crystal which are perpendicular to the x-direction considered and which contain the diffusing particles - here vacancies.

	We are only interested in the flux of vacancies in the x-direction, the diffusion current j of the vacancies. The flux or diffusion current of atoms that move via a vacancy mechanism, would have the same magnitude in the opposite direction.
		We do not assume equilibrium, but a space-dependent vacancy concentration cV( x, y, z). Being one-dimensional, we only assume a concentration gradient in the x-direction, cV(x, y, z) = c V(x).
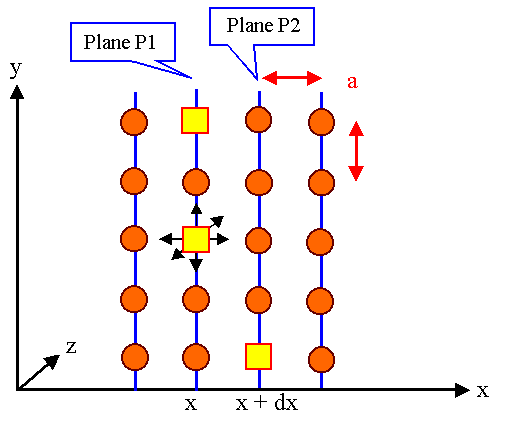
		On any lattice plane perpendicular to x we have a certain number of vacancies per unit area (the area density in cm–2), which is computable by c(x). We distinguish this particular concentration with the index of the plane; i.e. P1 is the number of vacancies on 1 cm2 area on plane No. 1, etc.
		We then have
		P1  =  a · cV (x)       P2  =  a · cV (x + dx)
		With dx = a = lattice constant, because smaller increments make no physical sense, we obtain
		P2  =  a · cV (x + a)
	Next we consider the jump rates in x-direction, i.e. that part of all vacancy jumps out of the plane that are in +x-direction. We define
		r1–2  =  jump rate in x – direction from P1 to P2   r2–1  =  jump rate in – x – direction from P2 to P1
		We obtain for our geometry:
		r1–2(T)  =  r2–1(T)  =     1  6   ·  r (T)
		This means that 1/6 of the total number of possible jumps of a vacancy is in the +x or – x direction, the other possibilities are in the y- or z-direction.
	The jump rate itself is given by the usual Boltzmann formula
		r  =  n0 · exp –   HM kT
		With n0 = vibration frequency of the particle, HM = enthalpy of migration.
	We obtain for the number of vacancies per cm2 and second, which jump from P1 to P2, i.e. for the component of the diffusion current j1–2 flowing to the right (and this is not yet the diffusion current from Ficks law!):
		j1–2  =  P1 · r1–2
		This is the current of vacancies flowing out in x-direction from P1. This current will be compensated to some extent by the current component j2–1 which flows into P1. This current component is given by
		j2–1  =  P2 · r2–1
		With the equation from above we obtain for the two components of the current
		j1–2  =   r  6  · a · c(x )     j2–1  =   r  6  · a · c(x  +  dx)
	The net jx current in x -direction, which is the current in Ficks laws, is exactly the difference between the two partial currents, we obtain
		jx  =   j1–2  –   j2–1          =    –  a · r 6 · {c(x + dx)  –  c(x)}
		If we now multiply by dx/dx = a/dx we obtain directly Ficks first law for one dimension:
		jx  =  –  a2 · r 6  ·   c(x + dx)  –  c(x) dx  =  –  a2 · r 6   ·   dc (x) dx
		All we have to do is to indentify (a2 · r)/6 with the diffusion coefficient D of Fick's first law; we then have it in full splendor:
		jx  =  –  D · dc(x) dx

	Ficks first law thus can be deduced in an unambiguous and physically sensible way for primitive cubic crystals in one dimension. (Mathematicians may have problems with the equality dx = a; but never mind).
		We also obtain an equation for the phenomenological diffusion coefficient D in terms of the atomic parameters lattice constants and jump rate (for the simple cubic lattice).
	Considering arbitrary crystals now is easy.
		The only parameters different in different crystal systems are the factor 1/6 and the jump distance, which does not have to be only a, but , in general, for jump type i will be Dxi. With i we enumerate all geometrically different variants of jumps and take into account that the x- component may depend on i.
		The diffusion coefficient then is given by
		D  =  g · a2 · r
		And g is a constant which is specific for the lattice under consideration, it is the so-called geometry factor of the lattice for diffusion.
	If we reconsider how we obtained the factor 1/6 for the cubic primitive lattice used above, it is clear that in a general case the geometry factor is defined by the equation
		g  = ½ · Si æ ç è Dxi a ö ÷ ø 2
		The factor 1/2 takes into account that only 1/2 of all possible jumps must be counted, because the other half would be the jumps back. Dxi/a simply expresses the component of the jump in x-direction in units of a .
		For simple lattices g is easily calculated; for the fcc and bcc lattice we have g = 1.
	Taking into account three dimension is easy, too:
		In isotropic lattices (which, besides the cubic lattices, covers all poly-crystals) no direction is special, the above equations are equally valid for the y- and z-direction. We obtain then a vector equation for Ficks first law
		j(r)  =  – D0 · exp – EM kt  · c (x,y,z)
	In anisotropic crystals things are messy. Every direction has to be considered separately, the so far scalar quantity D evolves into a second-rank tensor. Fortunately, we do not have to consider this here.

With frame

Exercise 3.1-1: Calculate the Geometry Factor

3.1.1 Diffusion and Point Defects

© H. Föll (Defects - Script)