 |
For obvious reasons some of the symbols deviate a little from the
symbols used in the text; e.g. we have hFP instead of HFP. |
| |
 |
We start with the system of equations that came from the
mass action law |
|
|
| |
|
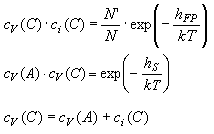 |
|
| |
 |
We start with the calculation of cv(C): |
|
 |
Inserting the first and the second equation into the third equation yields: |
| | |
| |
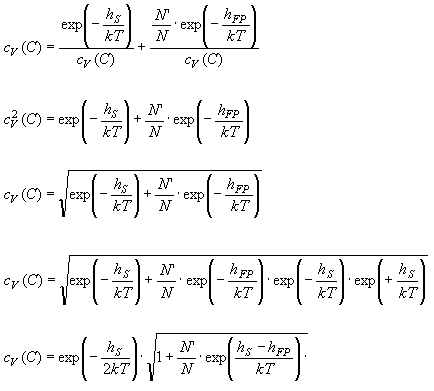 |
|
| |
 |
That was the first equation
for cV(C). Next we calculate ci(C). |
|
 |
Start with the third equation and eliminate cv(A) using the second. We have the final result
after a series of mathematical manipulations: |
|
| |
|
|
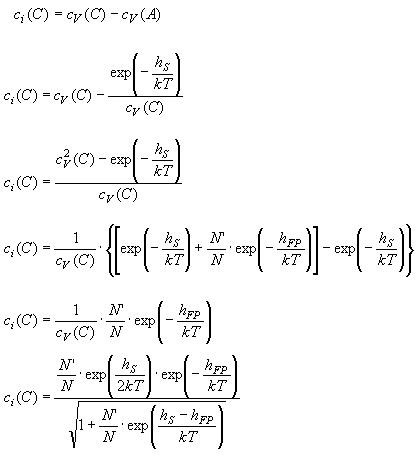 |
|
|
 |
That was the third equation.
Next we calculate cV(A). |
|
 |
Start with the third equation and eliminate ci(C) using the first, we obtain |
| | |
| |
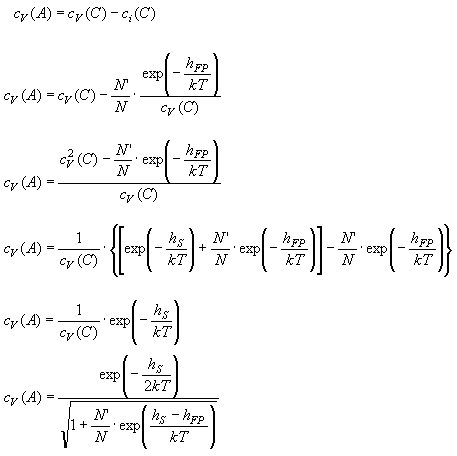 |
|
| |
 |
That's it. Nothing to it. ;-) |
|
 |
Well, not exactly. I myself certainly cannot solve problems like this without making some dumb mistakes in breaking
down the math. Almost everybody does. |
|
 |
However, I usually notice that I made a stupid mistake because the result just can't be true. And I can, if I really
employ myself, get the right result eventually - because I did some exercises like this before. And
that is why you should do it, too!. |
 |
As a last comment we may note that solving equations coming from the mass action
law can become rather tedious very quickly - compare the example in the
link, which is about as simple as it could be. |
|
| |
 |
Now we look at the limiting cases of pure Schottky or pure Frenkel disorder. |
|
 |
For pure Frenkel disorder we must have hFP << hS,
and cV(A) = 0. |
|
 |
For pure Schottky disorder we must have hFP >> hS, and ci(C)
= 0. |
 |
For the first case - pure Frenkel disorder - just look at the expression |
| |
æ
ç
è |
1 + | N
N' |
· exp |
hS – hFP
kT | ö
÷
ø
| 1/2 |
|
|
|
 |
For hS >> hFP, the exponential in this case is positive which means
|
| |
N
N' | · exp
| hS – hFP
kT | >> 1 |
|
|
|
 |
So you may neglect the 1 in the above expression and replace the whole square root by |
| |
|
|
 |
This gives for ci(C) |
|
|
| ci(C) | = |
N
N' | · |
æ
ç
è |
exp |
hS – 2hFP
kT
| ö
÷
ø |
1/2 |
æ
ç
è | exp |
hS – hFP
kT |
ö
÷
ø | 1/2 |
| = | N
N' |
· exp – | hFP
kT |
|
|
|
 |
This is the result as as it should be. |
 |
With this we immediately obtain |
| |
| cV(C) | = |
N
N' | · exp – |
hFP
2kT |
| | | |
| |
| cV(A) | = |
0 |
|
|
|
 |
This is so because |
|
|
N
N' |
· exp |
hS – hFP
kT | >> |
1 |
|
|
 |
Contrariwise, if hS << hFP, 1 + N/N'
· exp[(hS – hFP)/kT] » 1 obtains. |
|
 |
Because hS – 2hFP is a large negative number we get
|
| |
| ci(C) | = |
N
N' | · exp |
hS – 2hFP
2kT |
» | 0 |
|
|
|
 |
The expressions for cV(C) and cV(A) immediately reduce to the proper equation
|
| |
| cV(C) |
= cV(A) = exp – |
hS
2kT |
|
|
| | |
© H. Föll (Defects - Script)
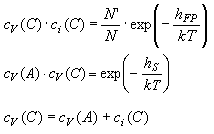
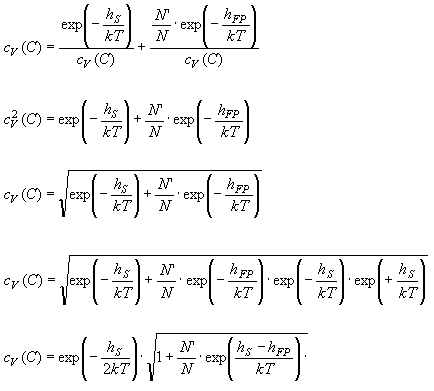
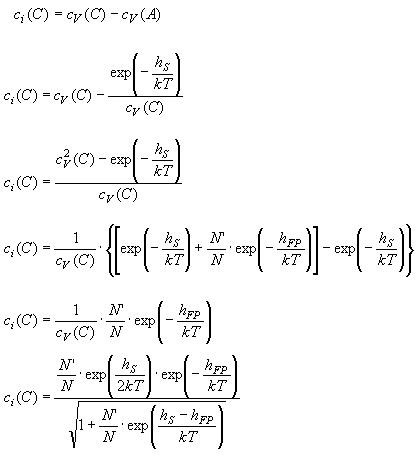
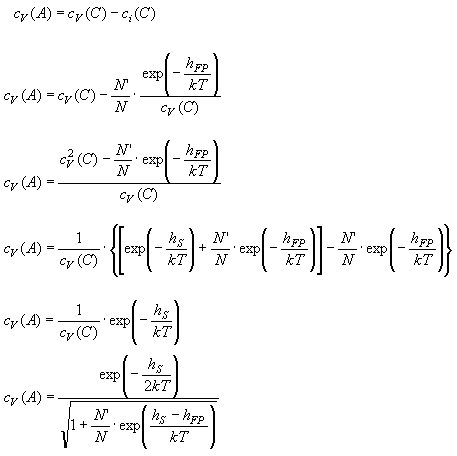
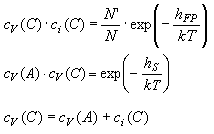
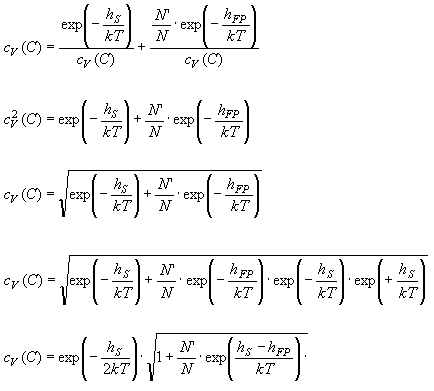
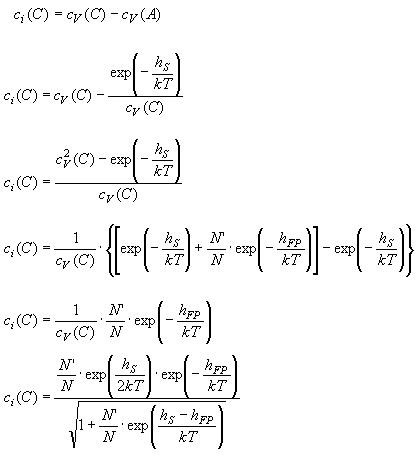
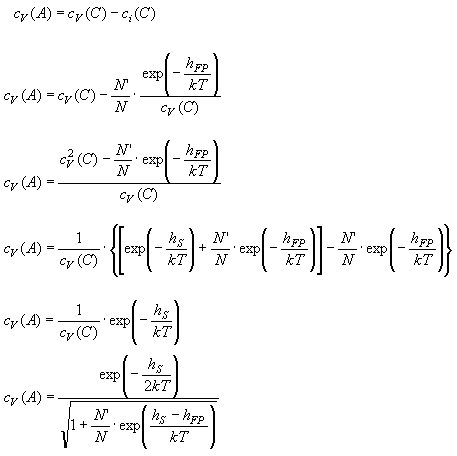
![]() Chemical Examples for Mass Action Law Applications
Chemical Examples for Mass Action Law Applications ![]() Exercise 2.2-1: Properties of Johnson Complexes
Exercise 2.2-1: Properties of Johnson Complexes