HTML-Facsimile
aus der ![]() (Sonderpreis im Funkschau Wettbewerb "Wissenschaft verständlich
dargestellt").
(Sonderpreis im Funkschau Wettbewerb "Wissenschaft verständlich
dargestellt").
Dr. Helmut Föll
Dr. rer. nat. Helmut Föll (32) studierte Physik an der Universität Stuttgart. Anschließend war er in den USA an der Cornell-Universität und im IBM-Forschungszentrum tätig. Seit 1980 beschäftigt er sich bei Siemens in München mit Materialfragen im Zusammenhang mit Silizium für Solarzellen.
Der Elektronenmikroskopiker wird oft gefragt: Kann man im Elektronenmikroskop Atome sehen? Die Antwort ist ein klares Jein: Man kann zwar keine einzelnen Atome sehen (schon deshalb nicht, weil es nichts gibt, um sie im Mikroskop festzuhalten), aber man kann manchmal etwas sehen, das auf einzelne Atome zurückgeht: z.B. dunkle Flecken, die von Uranatomen verursacht werden, welche auf einer sehr dünnen Kohlefolie liegen. Es ist auch schon möglich, schwere Atome in besonderen Molekülen mit der korrekten Geometrie abzubilden: Z. B. Quecksilberatome in einer metallorganischen Verbindung. Hat man aber einen Kristall als Präparat, dann sind alle Atome in einem regelmäßigen, dreidimensionalen Gitter angeordnet – und dieses Kristallgitter kann man unter günstigen Umständen direkt abbilden.
Was braucht man grundsätzlich, um Atome sehen zu können? Zunächst einmal eine Strahlung mit einer genügend kleinen Wellenlänge. Denn ein optischer Fundamentalsatz besagt, daß man nur dann zwei dicht benachbarte Objekte getrennt abbilden kann, wenn ihr Abstand größer ist als die Wellenlänge der zur Beobachtung herangezogenen Strahlung. Sichtbares Licht mit einer Wellenlänge von 500 nm ist also eine viel zu grobe Sonde, um in atomaren Dimensionen von der Größenordnung 0,2 nm etwas erreichen zu können.
Eine Strahlung, die in Frage kommt, sind Elektronenstrahlen. Elektronenstrahlen haben ausgeprägte Welleneigenschaften; die Wellenlänge ist um so kleiner, je höher die Geschwindigkeit der Elektronen ist. Schnelle Elektronen sind nun einfach herzustellen: das Prinzip ist von jeder Fernsehbildröhre her geläufig. Weiterhin kann man Elektronenstrahlen mit elektrischen oder magnetischen Feldern ablenken; dies ermöglicht den Bau von elektronenoptischen Linsen. Bei einer Beschleunigungsspannung von 100 kV beträgt die Wellenlänge des Elektronenstrahles 0,0037 nm; dem Bau eines hochauflösenden Elektronenmikroskopes steht somit prinzipiell nichts im Wege.
Bild 1 zeigt den schematischen Aufbau eines Elektronenmikroskopes. Erkennbar ist der Strahlkopf (Elektronenstrahlerzeugung), das Kondensorsystem (Fokussierung auf das Präparat), das Präparat, die abbildenden „Linsen" und schließlich ein Leuchtschirm. Die ganze Anordnung steht im Vakuum.
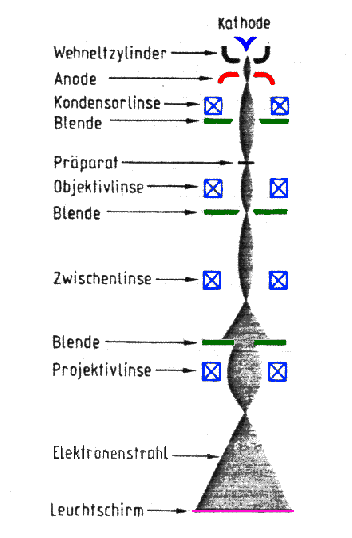
Bild 1. Prinzipieller Aufbau und Strahlengang eines Elektronenmikroskops
Die „Linsen" sind nichts anderes als Spulen mit einem speziell geformten Eisenkern. Das Magnetfeld dieser Spulen wirkt auf einen Elektronenstrahl wie eine gläserne Sammellinse auf Licht. Es ist eine recht schlechte Sammellinse, denn magnetische Linsen haben alle Linsenfehler, die auch bei optischen Linsen zu finden sind; als Stichworte seien angeführt: Astigmatismus, chromatische und sphärische Aberration.
Während man bei Glaslinsen diese Linsenfehler korrigieren kann, ist dies für magnetische Linsen prinzipiell nicht möglich – man muß mit ihren Fehlern leben. Dies führt zu einer Reihe von Forderungen an die technische Qualität eines Elektronenmikroskopes. Zum Beispiel muß die Hochspannung (typischerweise 100...200 kV) extrem stabil sein (= 10 ), ähnliches gilt für die Linsenströme. Trotzdem ist die günstigste Auflösung nicht viel besser als etwa 0,1 nm – eine Zahl, viel größer als die Wellenlänge des Elektronenstrahls.
Um verstehen zu können, wie das Bild eines Kristallgitters (oder eines biologischen Moleküls) entsteht, ist es zweckmäßig, zwei Bereiche getrennt zu betrachten:
1) Die Wechselwirkung des Elektronenstrahles mit dem Präparat, und
2) die Übertragungseigenschaften des elektronenoptischen Systems.
Normalerweise geschieht dies in der mathematischen Sprache des Optikers und bleibt dementsprechend völlig unverständlich für den Nicht-Fachmann. Deshalb soll hier der Versuch gemacht werden, die Bildentstehung im Elektronenmikroskop durch einfache elektrotechnische Begriffe zu beschreiben. Natürlich dürfen die Analogien nicht zu wörtlich genommen werden; auch kann nicht auf )jede Feinheit eingegangen werden.
Betrachten wir nochmals Bild 1. Wir beschreiben das Elektronenmikroskop nun folgendermaßen:
| Elektronenstrahlerzeugung und Fokussierung =entsp | Hf-Sender mit Richtantenne; |
| Präparat =entsp | Modulator der Hf; |
| Objektivlinse =entsp | Tuner, Demodulator und Vorverstärker; |
| restliche Linsen =entsp | Endverstärker; |
| Leuchtschirm =entsp | Ausgangswandler (z.B. Lautsprecher). |
Wir wollen schwache Signale sehr hoch verstärken, brauchen also ein hochwertiges System: einen frequenzkonstanten Sender(=entsp konstante Wellenlänge der Elektronen =entsp konstante Hochspannung), einen gut fokussierten, kohärenten Richtstrahl (=entsp gute Kondensoroptik) und eine gute Abstimmung des Empfängers (=entsp Linsenfokussierung; konstante Stromversorgung). Die erste Verstärkerstufe (=entsp Objektivlinse) ist natürlich die wichtigste; was sie nicht überträgt, geht verloren, und was sie an zusätzlichen Signalen produziert (=entsp Rauschen), wird am Ausgang das eigentliche Signal stören.
Der Anschaulichkeit halber nehmen wir als Präparat eine dünne Kristallscheibe, so dünn, daß sie nur eine Atomlage umfaßt. Die Annahme, daß nur zwischen den Atomen ein Durchkommen für die Elektronen möglich ist, ist leider falsch. Schnelle Elektronen können ein Atom mühelos durchdringen. Das elektrische Feld (das „Potential") der Atome ändert dabei die Phase der Elektronenwellen und lenkt gleichzeitig damit die Elektronen ein klein wenig ab.
Unsere Senderwelle wird also phasenmoduliert und der gerichtete Strahl wird etwas diffuser. Man braucht nun eine Beziehung zwischen der Objektstruktur und der entstandenen Phasenmodulation. Da man diese Beziehung nicht für alle denkbaren Objekte angeben kann, bedient man sich eines Tricks, der in der Elektrotechnik wohlbekannt ist: Man beschreibt das Objekt nicht in dem für uns am leichtesten zugänglichen „realen" Raum (in der Elektrotechnik entspräche dem ein Amplituden/Zeitdiagramm), sondern man gibt das Objektspektrum (entsprechend dem Frequenzspektrum) an.
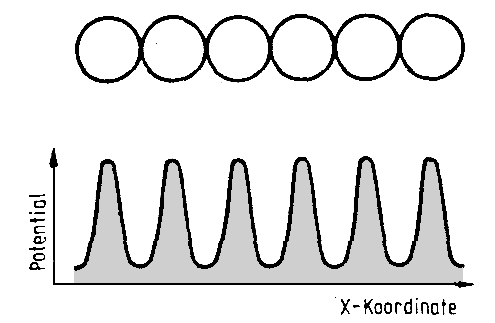
Bild 2 Eine Atomkette und ihr (vereinfachtes) Streupotential für Elektronen
Was ist nun ein Objektspektrum? Dazu betrachten wir ein einfaches eindimensionales Objekt, z.B. eine Kette von Atomen (Bild 2 oben). Für die Elektronen sind die Atome keine harten Kugeln, sondern geballte elektrische Felder, m denen sie abgelenkt oder gestreut werden. Das Streuvermögen eignes Atoms heißt Streupotential und läßt sich in einer Kurve darstellen, die in Bild 2 unten gezeigt ist. Das „Spektrum" dieser Kurve läßt sich nun genauso ermitteln wie das eines akustischen Wellenzugs.
Zur Veranschaulichung betrachten wir eine einfache Analogie: Ein Rechtecksignal in der Elektroakustik einerseits und einen rechteckigen Potentialverlauf, der unser Objekt darstellt, andererseits (Bild 3). Das Spektrum des Rechtecksignals ist bekannt; es besteht aus einer Grundfrequenz und einer Reihe von Harmonischen. Genau dasselbe Spektrum hat das Rechteck-Potential in einem Amplituden/Ortsfrequenz-Diagramm. Ähnlich wie das akustische Spektrum angibt, welche Frequenz mit welcher Stärke im Signal vorkommt, gibt das Ortsfrequenzspektrum an, welche Ortsfrequenzen (oder anschaulicher: welche Abstände zwischen Objektpunkten) mit welcher Häufigkeit auftreten. Hohe Ortsfrequenzen entsprechen dabei kleinen Abständen. Jedes Objekt kann durch ein eigenes Ortsfrequenzspektrum beschrieben werden.
Damit können wir nun die Modulation unserer Trägerwelle verstehen: Zu jeder im Präparat vorhandenen Ortsfrequenz gehört eine bestimmte Phasenmodulation und damit verbunden eine bestimmte Ablenkung der Senderwelle.
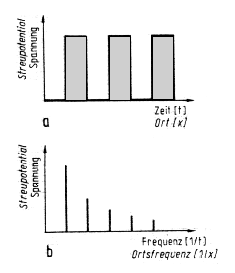 |
Bild 3. Ein Rechtecksignal und sein Spektrum, aufgefaßt entweder als Spannungsverlauf in der Zeit oder als Streupotential im Ort (kursive Beschriftung) |
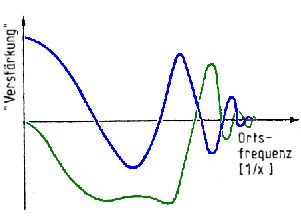 |
Bild 4. Kontrast-Transfer-Funktionen eines modernen Elektronenmikroskopes. Die zwei gezeigten Kurven entsprechen zwei verschiedenen Fokus-Einstellungen. Der Übergang von positiven zu negativen Werten bedeutet einen Obergang von „schwarz" zu „weiß" im realen Bild |
Die modulierte Hf trifft auf den Empfänger, im Elektronenmikroskop also auf die Objektivlinse. Zunächst einmal muß die Abstimmung stimmen. Die Linse muß auf das Objekt fokussiert sein. Am Ausgang der Objektivlinse soll ein verstärktes („vergrößertes") und demoduliertes Signal vorliegen, d. h. die Phasenmodulation soll in eine Amplitudenmodulation übergeführt werden. Die Demodulation erfolgt zwangsweise durch die Interferenz der verschiedenen Wellen nach dem Durchgang durch die Linse. Bei 0° Phasenverschiebung verstärken sich die Wellen, bei 180° Phasenverschiebung löschen sie sich aus.
Der entscheidende Punkt ist der Frequenzgang des Vorverstärkers bezüglich der im Signal enthaltenen Ortsfrequenzen. Ein guter Verstärker sollte einen geraden Frequenzgang haben, also alle Phasenverschiebungen unverfälscht übertragen. Das kann die Objektivlinse nun leider nicht. Auf Grund der Linsenfehler entstehen sogar noch zusätzliche Phasenverschiebungen, die außerdem noch sehr stark von der Abstimmung (d.h. von der Fokussierung) abhängen. So ist der Frequenzgang außerordentlich nichtlinear: Bild 4 zeigt ein Beispiel. Dieser Frequenzgang (oder wie es in der Physik heißt: die Kontrast-Transfer-Funktion) ist von überragender Bedeutung in der Hochauflösungsoptik.
 |
 |
 |
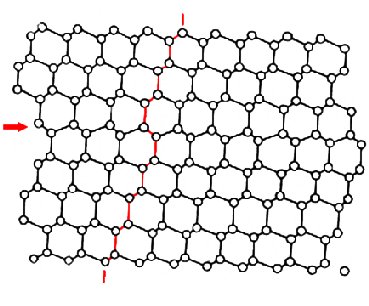
| Bild 5. a) Modellbild eines Si-Kristallgitters. Ein sogenannter Stapelfehler ist in der Bildmitte erkennbar | b) Elektronenmikroskopisches Bild eines Si-Kristalls mit Stapelfehler. Jeder weiße Punkt entspricht in erster Näherung einem Atompaar des Modellkristalls | c) Bild desselben Stapelfehler aber bei anderer Präparatdicke. Bedingt durch eine Dickenänderung des Kristalls erscheint das Bild sowohl verrauscht als auch "falsch" zu sein. |
Einen Stereoverstärker mit einem derartigen Frequenzgang würde man sicher zurückweisen, aber in der Elektronenmikroskopie gibt es nichts Besseres. Und es läßt sich damit leben – man darf nur keine allzu hohen Ansprüche haben. Bild 4 zeigt aber auch, daß es eine ganz bestimmte Abstimmung gibt, bei der der Frequenzgang in einem größeren Bereich halbwegs linear ist. Wenn man sich auf diesen Bereich beschränkt, kann man Bilder erhalten, die ein recht getreues Abbild des Objekts sind. Gefährlich sind die - Bereiche bei hohen Ortsfrequenzen, in denen Oszillationen auftreten: Dort werden bestimmte Objektdetails vollständig abgebildet, andere überhaupt nicht – das Abbild hat mit der Wirklichkeit nicht mehr viel zu tun.
Eine weitere Komplikation muß noch besprochen werden, bevor wir uns einigen Beispielen zuwenden. Bisher wurden nur ein- und zweidimensionale Objekte diskutiert, während wirkliche Präparate ja dreidimensionale Körper sind. Dünn müssen sie immer sein, aber eine Dicke von einigen zehn Atomlagen ist schon akzeptabel. In diesem Fall wird das dreidimensionale Objekt zunächst auf ein zweidimensionales reduziert, indem man sich alle Atome entlang des Elektronenstrahls auf eine Ebene projiziert denkt. Dabei wird natürlich nur dann noch etwas Vernünftiges übrigbleiben, wenn alle Atome genau untereinander liegen, der Elektronenstrahl also exakt parallel zu einer Kristallgitterkante einfällt. Man braucht also einen hochpräzisen Kippmechanismus, mit dem man das Präparat orientieren kann.
Da der Elektronenstrahl jetzt durch viele Atome läuft, wird er stärker moduliert werden. Die Modulation kann sogar stärker werden als die Trägerwelle; es ist, als ob die Amplitude eines Hf-Signals größer ist als die der Trägerwelle. Bei unserer Phasenmodulation treten insbesondere Phasenänderungen von mehr als 360° auf, 380° Phasenmodulation ist aber nicht unterscheidbar von einer Phasenmodulation von 20°. Die Konsequenz ist, daß mit steigender Präparatdicke sich das Bild des Objektes ändert und daß ein zu einer bestimmten Dicke gehörendes Bild bei größeren Dicken regelmäßig wiederkehrt. Dieser Dickeneffekt ist die Ursache der verschiedenen Bilder desselben Präparates wie in Bild 5 gezeigt: Zwischen 5b und 5c hat sich die Dicke des Präparates geändert. Bild 5a zeigt nun zum Vergleich das schematische Modell dieser Probe: Einen Siliziumkristall.
Man könnte nun fast meinen, hochauflösende Abbildungen im Elektronenmikroskop seien ein hoffnungsloser Fall. Daß dem nicht so ist, soll nun an einigen wenigen Beispielen aus der aktuellen Siliziumforschung gezeigt werden.

Bild 7. Die Grenzfläche zwischen Pd2Si (linker Teil) und Si.
Bei der Ionenimplantation von Si-Bauelementen werden Fremdatome gezielt in den Si-Kristall hineingeschossen. Dabei wird das Kristallgitter schwer geschädigt, die obere Schicht des Kristalles wird meistens sogar amorph. Von grundsätzlichem Interesse ist dabei die Struktur der Grenzfläche zwischen kristallinem und amorphem Bereich und die Art der durch die Bestrahlung verursachten Kristallgitterdefekte; Fragen, die nur mit hochauflösender Elektronenmikroskopie zu beantworten sind.
Bild 6 zeigt Beispiele: In Bild 6a ist die Grenzfläche amorph – kristallin zuerkennen und in Bild 6b einige der entstandenen Gitterdefekte. Aus diesen Bildern läßt sich sofort entnehmen, daß der Übergang amorph – kristallin sehr abrupt und nicht sehr rauh ist.
Ein letztes Beispiel aus einem sehr aktuellen Forschungsgebiet zeigt Bild 7. Gezeigt ist ein sogenannter Silizidkontakt für die Höchstintegration. Der Obergang von Siliziumkristall zum Pdsi-Silizid-Kristall ist sichtbar. An diesem Übergang stoßen zwei verschiedene Kristallgitter zusammen und ein Verständnis der Struktur der dabei entstandenen Grenzfläche ist überaus wichtig für künftige Bauelemente und für die Grundlagenforschung.
Hochauflösende Elektronenmikroskopie kann also trotz der enormen grundsätzlichen und technischen Schwierigkeiten wichtige Beiträge zum Verständnis des Aufbaus der Materie erbringen. Gerade im Bereich der Halbleitertechnologie wird sie uns noch viele faszinierende Einblicke in den Mikrokosmos der Kristalle ermöglichen und somit dazu beitragen, immer kompliziertere Schaltungen auf immer kleinerem Raum zu ermöglichen.
Veröffentlicht in der
![]() , HTML-Version
1/97
, HTML-Version
1/97
Verfasser:
Prof. Dr. H. FÖLL (E-Mail)
zurück zu Kapitel 6.3.4