The golden section search method in one dimension is used to find a minimum for a unimodal continuous function of a single variable over an interval without using derivatives. Unimodal in \([a,b]\) means having only one extremum in \([a,b]\). The idea is similar to the bisection method for finding a zero: narrowing the interval containing the minimum (being called a bracketing interval) until a specified accuracy is reached. When doing so, we want two things:
an optimal reduction of the size of the bracketing interval and
a minimal number of function calls.
How to iteratively approach a minimum of a function \(f\)? If for a given interval \([a,b]\) there is some point \(c\in[a,b]\) so that \(f(c) \lt f(a)\) and \(f(c) \lt f(b)\), then \([a,b]\) brackets a minimum of \(f\), and \(c\) is an approximate value (estimate) for the minimum point of \(f\).
That situation given, to reduce the interval size one chooses a further value \(d\in[a,b]\). If \(f(d) \gt f(c)\), \(d\) becomes a new interval limit and replaces either \(a\) or \(b\) (depending on which side of \(c\) it lies) while \(c\) remains the best estimate. If \(f(d) \lt f(c)\), the same goes for \(c\) as new boundary; then, \(d\) becomes the new best estimate.
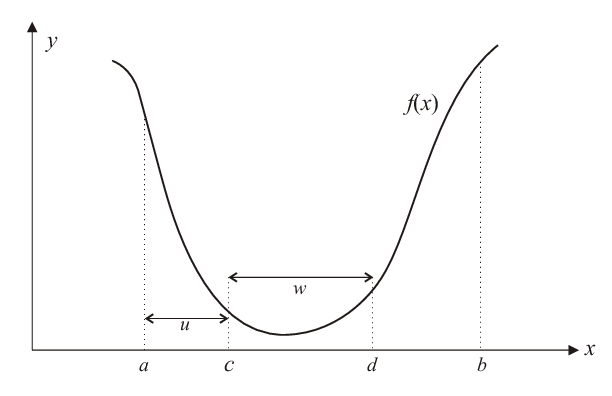
But how to choose both \(c\) and \(d\) most effectively? Suppose that \(c \lt d\) (cf. Fig. 4.2) and consider the following interval lengths: of the full interval \(\ell = b - a\), of the parts \([a,c]\) and \([c,b]\),
|
| \begin{equation*} u={c-a} \ \text{ and } \ \ell-u={b-c}\,, \end{equation*} | (4.1) |
as well as the position of \(d\) with respect to \(c\),
|
| \begin{equation*} w={d-c}\,. \end{equation*} | (4.2) |
From the above it is clear that in the next iterative step, the bracketing interval will either be of size \(u + w\) or \(\ell - u\). In order to have the same “gain” for both cases one has to choose \(w\) as to make these equal, i.e.
|
| \begin{equation*} u+w=\ell-u \ \ \Rightarrow \ \ w=\ell-2u. \end{equation*} | (4.3) |
This implies a symmetric choice of the interior points \(c\) and \(d\).
Now, to determine which \(u\) is optimal, one assumes that it has been determined in the previous step by the same strategy. This means that the placement of \(d\) relative to \(c\) and \(b\) should be the same as that of \(c\) relative to \(a\) and \(b\). This leads to the condition
|
| \begin{equation*} \frac{w}{\ell-u}=\frac{u}{\ell}\,. \end{equation*} | (4.4) |
Using \(w=\ell-2u\), this reads
|
| \begin{equation*} \frac{\ell-2u}{\ell-u}=\frac{u}{\ell}\,. \end{equation*} | (4.5) |
In terms of the relative length \(u'=u/\ell \lt 1\) one therefore has that
|
| \begin{equation*} 1-2u'=u'(1-u') \end{equation*} | (4.6) |
or
|
| \begin{equation*} (u')^2 - 3u' + 1 =0\:\!, \end{equation*} | (4.7) |
which has the solution
|
| \begin{equation*} u'_{\text{opt}}=\frac{3-\sqrt{5}}{2}\approx 0.381966. \end{equation*} | (4.8) |
This means that if this strategy is followed right from the beginning, in each iterative step the bracketing interval will shrink to \(1-u'_{\text{opt}}\approx 61.8\) % of its previous size. Therefore, this method converges linearly, and the rate of convergence is approximately 0.618. Since this result is related to the golden section number \(\varphi = (1+\sqrt{5})/2\) by \(1-u'_{\text{opt}} = \varphi-1 = \varphi^{-1}\), this method is called “golden section search”.
It remains to discuss the criterion for terminating the iteration. Close to a minimum \(x_{\text{min}}\), a function is rather flat, which influences the accuracy to which the minimum can be located. Consider the Taylor expansion of a function \(f\) close to its minimum:
|
| \begin{equation*} f(x) \approx f(x_{\text{min}}) + \frac{1}{2}f''(x_{\text{min}})(x-x_{\text{min}})^2. \end{equation*} | (4.9) |
According to the above discussion about numerical accuracy (Sect. 4.2, remark 4), a deviation of \(f(x)\) from \(f(x_{\text{min}})\) is numerically detectable only in terms of the relative error. Therefore, for a deviation given by
|
| \begin{equation*} \left|\frac{f(x)-f(x_{\text{min}})}{f(x_{\text{min}})}\right| \lt \delta \end{equation*} | (4.10) |
one has that
|
| \begin{equation*} \frac{1}{2}f''(x_{\text{min}})(x-x_{\text{min}})^2 \lessapprox \delta|f(x_{\text{min}})| \end{equation*} | (4.11) |
or
|
| \begin{equation*} |x-x_{\text{min}}| \lessapprox \sqrt{\delta}\;\sqrt{\frac{2|f(x_{\text{min}})|}{f''(x_{\text{min}})}}\,, \end{equation*} | (4.12) |
so that the relative deviation of \(x\) from the minimum can be expressed as
|
| \begin{equation*} \frac{|x-x_{\text{min}}|}{|x_{\text{min}}|} \lessapprox \sqrt{\delta}\;\sqrt{\frac{2|f(x_{\text{min}})|}{x_{\text{min}}^2\,f''(x_{\text{min}})}}\,. \end{equation*} | (4.13) |
The final square root is a constant that, according to Press et al., “for most functions … is a number of order unity”.2 (If it is not, it can be made so without changing the position of the minimum.) Therefore, it follows that
|
| \begin{equation*} \frac{|x-x_{\text{min}}|}{|x_{\text{min}}|} \lessapprox \sqrt{\delta}\,, \end{equation*} | (4.14) |
i.e., the minimum of the function can be found only up to an accuracy that is given by the square root of the relative deviation of the function values. In other words, the interval containing the minimum can best be bracketed up to a size of \(\sqrt{\mathtt{eps}}\) times the minimum position (with the machine precision eps); it is completely useless to demand a better result.
There are several other algorithms for finding a minimum in one dimension, and similar to the bisection method for finding zeros, the golden section search is slow but safe. In an implementation it can therefore serve as the “fall-back routine” if faster methods fail.
Additionally, any one-dimensional minimization algorithm can also be used as a “sub-algorithm” for minimization in higher dimensions where a certain search direction is determined by the main algorithm.3
2W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery, Numerical Recipes, chapter “Minimization or Maximization of Functions”
3For an illustration of such a situation, have a look again at figure 4.1.
© J. Carstensen (Comp. Math.)