Figure 4.1:
The upper part shows a contour plot of a real-valued function of two variables \(x_1\),
\(x_2\), and a sectioning line defining the plot shown in the lower part. The global and a local minimum are
indicated.
In general, numerical optimization refers to choosing the optimal values of variables or parameters among available alternatives. It comprises a wide area of mathematical problems and numerical techniques.1 Since the term “optimization” has no meaning by its own, it must always be specified which quantity or property shall be optimized, and what its optimum is considered to be like. Rather frequently, optimization requires to find an extremum of a certain function, usually called the objective function. The objective function may depend just on one, or on several, or on a great many variables. Sometimes, further constraints apply as well.
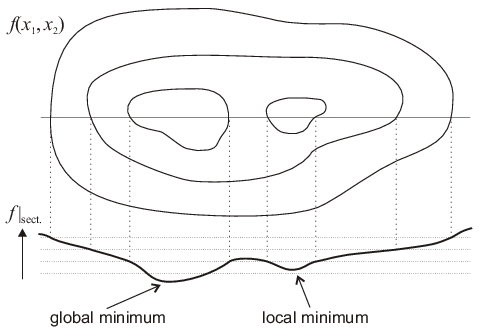
In general, it suffices to know how to search for a minimum, because in case that a function \(f\) has a maximum, then \(-f\) has a minimum. Minimization of a real-valued function means to find those value(s) of its variable(s) for which it attains its lowest function value. This minimum value is called the global minimum of the function. Besides that, if one looks only at a limited range of the variable(s) one may also find a minimum which—if it is not located on the boundary of that range—is called a local minimum; however, it can have a higher value than the global one (cf. Fig. 4.1).
In this chapter, two examples related to numerical optimization are treated: one-dimensional minimization by golden section search and multi-dimensional minimization for the special case of the linear least squares method (used for fitting of data).
1For an overview, see http://en.wikipedia.org/wiki/Optimization_%28mathematics%29.
 |
 |
 |
 |
© J. Carstensen (Comp. Math.)