Figure 3.3:
Newton method (two iterations). \(\bar{x}\) is the searched-for zero.
Compared to the interval bisection method, this algorithm to find the zero \(\bar{x}\) of a function has the advantage that it shows much faster convergence (quadratic instead of linear). However, it has two severe drawbacks: Convergence is not always guaranteed, and one needs to determine the derivative of the function under investigation. Therefore, it is not often in practical use in its pure form. It is, however, very instructive to understand the basics of this algorithm, its convergence behavior, and why it may fail. That’s why it is discussed here.
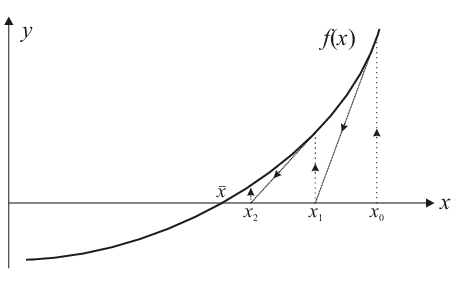
Consider a function \(f(x)\) being approximated by its tangent at \(x_0\). The zero \(x_1\) of this tangent [which exists if \(f'(x_0)\neq0\)] is an approximation for \(\bar{x}\). To determine \(x_1\) we express the slope of the tangent as
|
| \begin{equation*} f'(x_0)=\frac{f(x_0)}{x_0-x_1} \ \Rightarrow \ x_0-x_1=\frac{f(x_0)}{f'(x_0)} \ \ \Rightarrow \ \ x_1=x_0-\frac{f(x_0)}{f'(x_0)}\,. \end{equation*} | (3.14) |
This procedure is repeated with \(x_1\) instead of \(x_0\) to obtain an approximation \(x_2\), and so on; for a graphical representation see Fig. 3.3. Obviously, the iteration formula for the Newton method is
|
| \begin{equation*} \label{eq:Newtoniter} x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}, \ \ n\in\mathbb{N}_0\,, \ \ f'(x_n)\neq0\,. \end{equation*} | (3.15) |
Compared to the formalism for fixed-point determination, this corresponds to the problem \(g(x)=x\) with \(g(x)=x-f(x)/f'(x)\). Therefore, according to the Banach fixed-point theorem, the Newton algorithm converges if \(|g'(x)|\leq q \lt 1\), or
|
| \begin{equation*} \left|\frac{f(x)f''(x)}{[f'(x)]^2}\right|\leq q \lt 1\,, \end{equation*} | (3.16) |
holds in a certain interval containing the zero. Note that the Banach fixed-point theorem
can yield linear convergence only. However, as will not be proved here, the Newton algorithm has quadratic convergence.
The two main disadvantages of the Newton method are (i) the necessity to start the iteration rather close to the searched-for
zero in order to achieve convergence and (ii) to calculate the inverse of the derivative at each iterative step. As long
as one deals with functions of a single variable only, this is not severe, but for several variables the effort increases
significantly.
The two main disadvantages of the Newton method are (i) the necessity to start the iteration
rather close to the searched-for zero in order to achieve convergence and (ii) to calculate the inverse of the derivative
at each iterative step. As long as one deals with functions of a single variable only, this is not severe, but for several
variables the effort increases significantly.
On the other hand, the general aspect of using the derivative to determine the correct search direction is helpful in higher dimensions, and combined with a different method to determine the step size and to guarantee convergence (as, e.g., bisection) one obtains a method that works reliably and shows a super-linear convergence behavior. (If \(\left|\bar{x}-x_{n+1}\right|\leq M\left|\bar{x}-x_n\right|^p\), \(p\gt 1\), then the sequence \(\{x_n\}\) is convergent of order \(p\).)
 |
 |
 |
 |
© J. Carstensen (Comp. Math.)