Figure 3.2:
Secant algorithm (three iterations). \(\bar{x}\) is the searched-for zero.
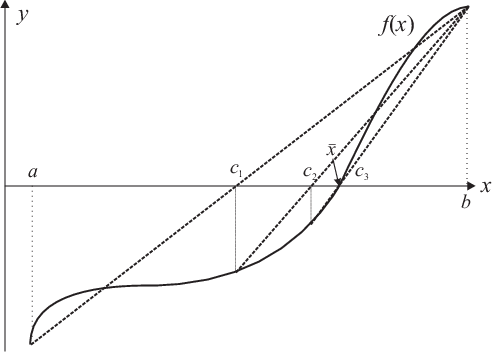
As nearly true in general, knowing more about a problem one can solve it more efficiently. For the case of the secant algorithm we do not know more about the function for which to find an zero, but we assume more about the function, i.e. it resembles nearly a linear function close to the zero position. As shown in the example in Fig. 3.2 solving for the zero of the secant connecting the limiting points of the search interval can be an efficient strategy to be more efficient than the bisection method. The mathematical equation for this is
|
| \begin{equation*} x_i = a - \frac{f(a)*(b-a)}{f(b)-f(a)}\,. \end{equation*} | (3.13) |
Of course there are many examples of functions for which the secant algorithm is much more inefficient than the bi sectioning method. So most often really efficient zero finding algorithms are a combination of several methods including an sophisticated strategy to identify the most efficient approach or combining the results of all algorithms.
 |
 |
 |
 |
© J. Carstensen (Comp. Math.)