In what follows we will discuss possible arrangements of particles in states, i.e. configurations,
and the probabilities to find these arrangements. The reason for this is quite simple: The most probable configuration(s)
will be found in nature, i.e. thermodynamic systems. This is a quite obvious statement but it is the key for understanding
entropy and all properties of classical thermodynamics as discussed up to now.
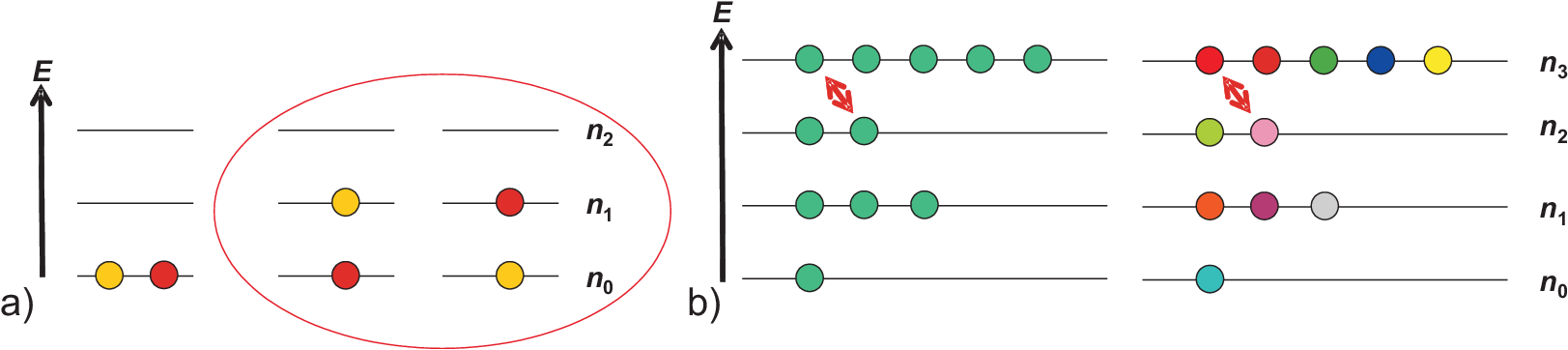
Fig. 5.1 a) shows an example of different arrangements of two particles
in a three level system. Some general features can be seen:
Energy levels are labeled by integer numbers \(i = 0, 1, 2\)
Each energy level has an energy \(\epsilon_i\) with typically \(\epsilon_0 = 0\) (by convention)
\(n_i\) labels the occupation numbers of each energy level
A configuration is the overall set of occupation numbers \(\{n_0, n_1, n_2\}\)
In our example two configuration are shown: \(\{2, 0, 0\}\) vs. \(\{1, 1, 0\}\). Obviously the configuration \(\{1, 1, 0\}\) has a larger weight \(W = 2\) (number of arrangements for occupying states in one configuration) than \(\{2, 0, 0\}\) with \(W = 1\). But several aspects have been neglected for the comparison of both configurations:
Both configurations differ in the overall energy, and thus in their temperature dependence
Particles have been assumed to be distinguishable, otherwise configuration \(\{1, 1, 0\}\) would have the same weight \(W = 1\) as configuration \(\{2, 0, 0\}\).
Fig. 5.1 b) emphasizes the dependence of weights on the nature of particles, i.e. if they are distinguishable or indistinguishable. To be principally indistinguishable is a property of quantum mechanical particles, which is not so easy to understand and with dramatic consequences for many particle systems, some of which we will discuss as well here. For the moment is is enough to take indistinguishable as identical and distinguishable as non-identical particles.

Obviously for non-identical particles many more arrangements exist which for the example in Fig. 5.1 b) can be calculated easily
The following table shows for a four level system two configurations of 10 non-identical particles which have the same overall energy.
level \(i\) | \(n_i\) | \(E_i\) | \(n_i E_i\) |
3 | \(0 \qquad \;\,1\) | 4 | \(0\;\, \qquad 4\) |
2 | \(0 \qquad \;\,2\) | 3 | \(0\;\, \qquad 6\) |
1 | \(10 \qquad 3\) | 2 | \(20 \qquad 6\) |
0 | \(0 \qquad \;\,4\) | 1 | \(0\;\, \qquad 4\) |
| \( \sum n_i= 10\) |
| \(\sum n_i E_i = 20\) |
According to Eq. (5.1) the weight for configuration \(\{0, 10, 0, 0\}\) is
|
| \begin{equation*} W = \frac{10!}{10!} = 1 \quad . \end{equation*} | (5.2) |
The weight for configuration \(\{4, 3, 2, 1\}\) is
|
| \begin{equation*} W = \frac{10!}{1! 2! 3! 4!} = 12600 \quad , \end{equation*} | (5.3) |
so even under the restriction of two states having the same overall energy large differences
in the weights can exist. Configuration \(\{0, 10, 0, 0\}\) is much less probable than configuration \(\{4, 3, 2, 1\}\).
To find the full solution for weights of distinguishable particles (i.e. classical
particles) we have to introduce the degeneracy of an energy level \(g_i\). According to the above definition
\(i\) indicates states with different energies, but several states may have the same energy. For example without
magnetic fields states with spin up and spin down have the same energy, so the degeneracy is \(g = 2\). The
same is true for electrons in atomic orbitals having the same quantum number \(l\). The degeneracy is \(g = (2 l + 1) 2\); here the last factor 2 takes into account the two spin orientation. In summary the weight \(W_i\) to occupy energy level \(i\) for distinguishable particles can be calculated as follows:
The weight for arranging \(N\) distinguishable particles in a configuration \(\{n_0, n_1, \cdots\}\) is
|
| \begin{equation*} W = \frac{ N!}{\prod_i n_i!} \label{Maxwell_Boltzmann_weight_1} \end{equation*} | (5.4) |
Taking into account a possible degeneracy \(g_i\) of each energy level \(i\) the weight increases to
|
| \begin{equation*} W = \frac{ N! \prod_i (g_i)^{n_i}}{\prod_i n_i!} \label{Maxwell_Boltzmann_weight_2} \end{equation*} | (5.5) |
As we learned from the Gibbs paradox even classical particles must be assumed to be ”somehow non distinguishable”. This can be achieved by omitting \(N!\) in the weight leading to
|
| \begin{equation*} W = \frac{\prod_i (g_i)^{n_i}}{\prod_i n_i!} \label{Maxwell_Boltzmann_weight} \end{equation*} | (5.6) |
This is the weight for the famous Maxwell-Boltzmann distribution. It holds for classical particle at ”normal” temperatures and ”normal” masses.
Bosons are quantum mechanical particles, i.e. principally indistinguishable, for which each energy level can be occupied with an unlimited number of particles (because they have a symmetric quantum mechanical many particle state function). An example for the distribution of \(n_i\) bosons in one energy level \(E_i\) with a degeneracy \(g_i\) is shown in Fig. 5.2. The \(g_i - 1\) vertical lines indicate the limits of the degenerate states.
The \(n_i\) circles indicate the particles being arranged into states as indicated by the vertical lines. Any arrangement of circles and vertical lines is an allowed configuration and the number of these arrangements is \((n_i+g_i - 1)!\). Interchanging the \(n_i\) particles gives always the identical state, the same is true for the \(g_i-1\) vertical lines. So the weight for occupying this state is
|
| \begin{equation*} W_i = \frac{(n_i+g_i-1)!}{n_i! (g_i-1)!} \quad , \end{equation*} | (5.7) |
leading to the overall weight, i.e. the weight of the Bose-Einstein distribution,
|
| \begin{equation*} W = \prod_i W_i = \prod_i \frac{(n_i+g_i-1)!}{n_i! (g_i-1)!} \label{Bose_Einstein_weight} \quad . \end{equation*} | (5.8) |
Fermions are quantum mechanical particles, i.e. principally indistinguishable, for
which each energy level can only be occupied once (because they have an antisymmetric quantum mechanical many particle state
function). As outlined before, e.g. the two spin states are taken into account by the degeneracy \(g_i\).
Distributing \(n_i\) fermions in one energy level \(E_i\) with a degeneracy \(g_i\)
can be described as follows:
The first particle we can put into any of the \(g_i\) states.
The second particle can be put into any one of the remaining \(g_i - 1\) states. So the weight \(W_i\)
is given by
|
| \begin{equation*} W_i = g_i (g_i - 1) (g_i - 2) ...(g_i-n_i+1) = \frac{g_i!}{(g_i-n_i)!} \quad , \end{equation*} | (5.9) |
leading to the overall weight, i.e. the weight of the Fermi-Dirac distribution,
|
| \begin{equation*} W = \prod_i W_i = \prod_i \frac{g_i!}{(g_i-n_i)!} \label{Fermi_Dirac_weight} \quad . \end{equation*} | (5.10) |
© J. Carstensen (TD Kin II)