Figure 4.1:
Binary phase diagram with obvious errors according to the Gibbs phase rule.
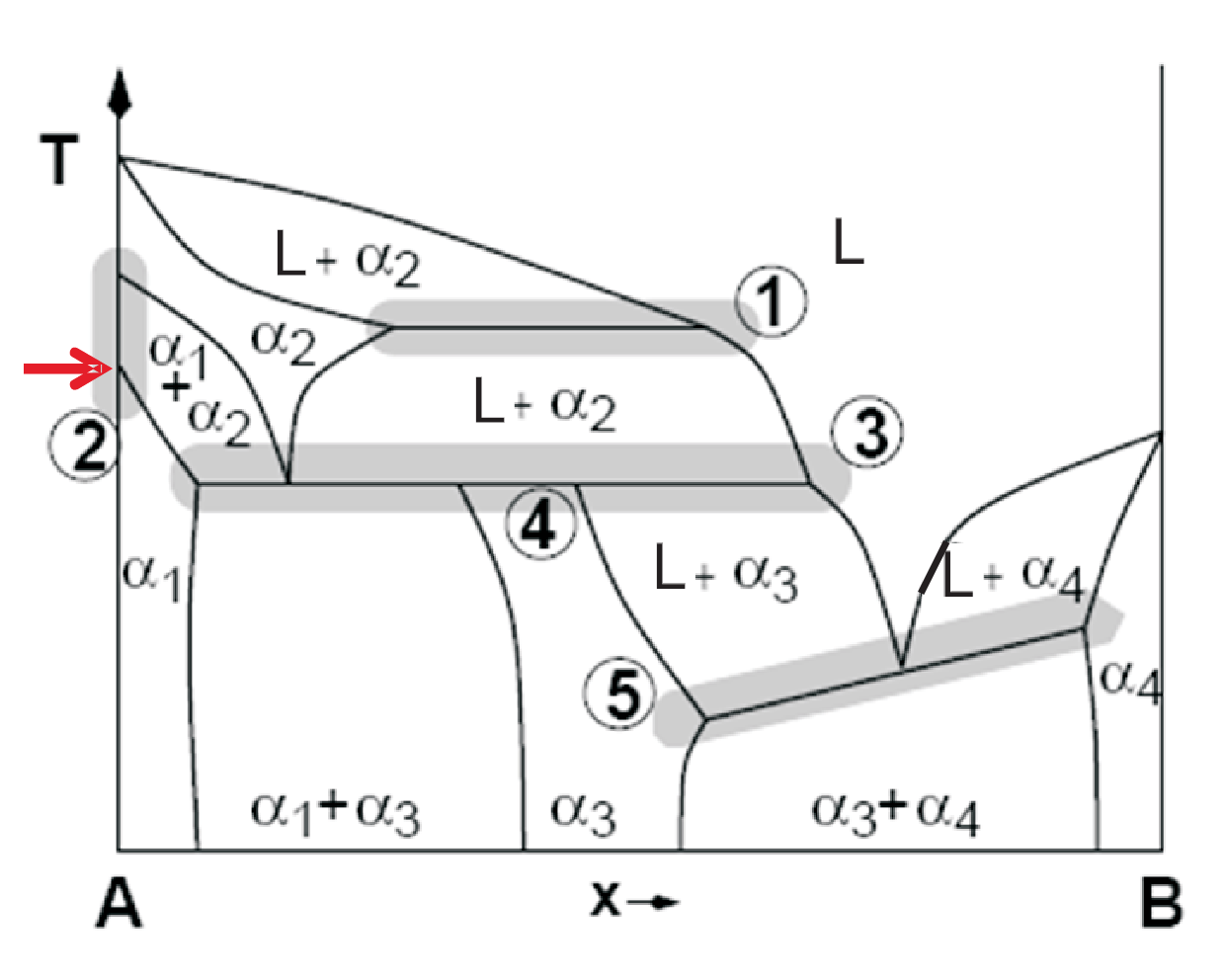
To see how rigorous the Gibbs phase rule is we will discuss the artificial binary phase diagram shown in Fig. 4.1. Since we have a binary phase diagram \(C = 2\). The shown \(x - T\) diagram implies \(p = const.\), i.e. \(P + F = C + 1 = 3\) or \(F = 2 + 1 - P\), thus the maximum number of coexisting phases is 3, i.e. \(F = 0\) which marks a point or horizontal line in the phase diagram. \(F = 1\) marks a sloped line or heterogeneous field. \(F = 2\) marks a homogeneous field.
With this input we now check the lines highlighted in Fig. 4.1.
The horizontal line implies \(F = 0\), however we only have two phases (L and \(\alpha_2\)), i.e. \(P = 2\) but \(P = 3\) needed! No phase boundary can exist between two identical fields (L and \(\alpha_2\)).
This vertical line holds for pure A, i.e. \(C = 1\). Thus having two phases \(F = 0\) is a must, however \(T\) can be varied. Such errors can be induced experimentally by overlooking impurities, i.e. not pure A exists.
A) Neighboring closed areas can not contain more than \(\pm 1\) different phases in contradiction to two neighboring phases \((L + \alpha_2)\):\((\alpha_3)\), B) The max. number of coexisting phases is three in contradiction to two neighboring phases \((L + \alpha_2)\):\((\alpha_1 + \alpha_3)\).
Since \(P = 3\) \((L,\; \alpha_2)\) \(\alpha_3\) we expected \(F = 0\), however \(x\) can be varied.
Three phases (e.g. \(L\), \(\alpha_3\), \(\alpha_4\)) can only coexist at constant \(T\) and \(x\), i.e. \(F = 0\). Thus a horizontal line with \(T = const.\) must exist and no slope is allowed.
Gibbs phase rule including chemical reactions and other restraints
© J. Carstensen (TD Kin I)
With frame