Kinetics of a bottle with sparkling water

6.3 Kinetics of a bottle with sparkling water

We will discuss many aspects of kinetics and transport using the well known example of a bottle with sparkling water. Everybody knows the phenomena:

When shaking the bottle instantly pressure builds up. Many gas bubbles occur in the water moving upwards.
When you open now the bottle not only gas is leaving but a mixture of water and gas which nicely wets the surrounding.
When you wait ”long enough” the pressure is gone again.
When the bottle is not closed completely a continuous small gas flow will slowly reduce the concentration of carbon acid in the water.

These are the obvious effects. But transport and kinetics deals with many more aspects in our example:

Why do gas bubbles form in the water?
Why do gas bubbles grow in size?
Why do gas bubbles stick at the bottle walls?
Why do gas bubbles move upwards?
Why does shaking increase the pressure, resp. lead to a formation of \({\rm CO_2}\) in the water?
Why are the time constants for increasing and decreasing the pressure so different?

Figure 6.1: Schematic of bottle with sparkling water

We will tackle all these aspects, but only phenomenologically, i.e. we will not discuss the microscopic mechanisms/concepts (this will be the topic of the summer term). We will learn fundamental concepts to simplify the modeling for answering certain aspects. So it is not necessary to understand and quantify all aspects of transport and kinetics for describing several phenomena. This discussion focuses on ”rate determining” steps which are actually the slowest parts in a transport chain and not (as one may assume naively) the fastest steps with the strongest driving forces.
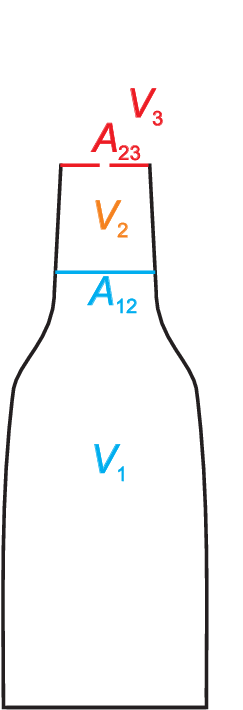
Our first calculation will already illustrate nearly all relevant features of a phenomenological description. Let us discuss the situation after shaking the bottle when a high pressure is within the bottle and a high concentration of \({\rm CO_2}\) is in the vapor phase in the top part of the bottle. This is illustrated schematically in Fig. 6.1. Let \(I_1, I_2, I_3\) be the number of moles of \({\rm CO_2}\) molecules in the water phase, in the vapor phase, and leaving the bottle through a possible opening, respectively. Let \(p_1, p_2, p_3\) be the corresponding partial pressures, \(V_1, V_2, V_3\) the corresponding volumes of the phases, and \(A_{12}\) the area of the interfaces between water and vapor and \(A_{23}\) the area of a possible opening between the vapor phase and the surrounding.
We will discuss the kinetics according to the following scheme

\begin{equation*} \text{I}_1 \xrightleftharpoons[k_3]{k_1} \text{I}_2 \xrightarrow{k_2} \text{I}_3 \quad . \label{reaction_scheme} \end{equation*}

(6.10)

Don’t bother; you will understand this scheme soon. As discussed in section 4.1 for the Gibbs phase rule in thermodynamic equilibrium partial pressures in all phases of all components are identical. Quite intuitively (and proved in summer term) gradients (differences) in (partial) pressures are the driving forces to reach thermodynamic equilibrium, for several transport processes, and for the kinetics of e.g. chemical reactions. Thus we can write

\begin{equation*} \frac{dI_1}{dt} = \alpha A_{12} \left( p_2 - p_1 \right) \quad . \end{equation*}

(6.11)

Of course the rate of change of \(I_1\) (the amount of carbon dioxide in water) scales with the area of the interface \(A_{12}\); \(\alpha\) is just a scaling factor. Let us assume simply Raoult’s law \(p_1 = c_1\; p_1^0\) and \(p_2 = c_2\; p_2^0\) where \(c_1 = I_1 / V_1\) and \(c_2 = I_2 / V_2\) are the corresponding concentrations of \({\rm CO_2}\). Finally we get

\begin{equation*} \frac{dI_1}{dt} = \alpha A_{12} \left( \frac{I_2}{V_2} p_2^0 - \frac{I_1}{V_1} p_1^0 \right) = - k_1 I_1 +k_3 I_2 \quad \mbox{with} \quad k_1 = \frac{A_{12}}{V_1} p_1^0 \alpha \quad\mbox{and}\quad k_3 = \frac{A_{12}}{V_2} p_2^0 \alpha \quad . \label{kin_1} \end{equation*}

(6.12)

Eqs. (6.12) now define the first part of the scheme \({\rm I}_1 \underset{k_3}{\overset{k_1}{\rightleftharpoons}} {\rm I}_2\). \(k_1\) and \(k_3\) are kinetic coefficients. Easily we found some fundamental aspects about such kinetic coefficients:

Typically geometry parameters, e.g. volume, area, distances, are part of kinetic coefficients.
Back and forward reaction kinetics often differ, i.e. \(k_1 \neq k_3\).

Now we can complete the set of kinetic equations

\begin{equation*} \frac{dI_2}{dt} = k_1 I_1 - k_3 I_2 - k_2 I_2\quad \mbox{and} \quad \frac{dI_3}{dt} = + k_2 I_2 \label{kin_3} \end{equation*}

(6.13)

with a last definition

\begin{equation*} k_2 = \frac{A_{23}}{V_3} p_3^0 \beta \quad .\label{kin_4} \end{equation*}

(6.14)

Note that we introduced a new scaling factor \(\beta\) for the transport from the vapor phase into the surrounding (Why?).