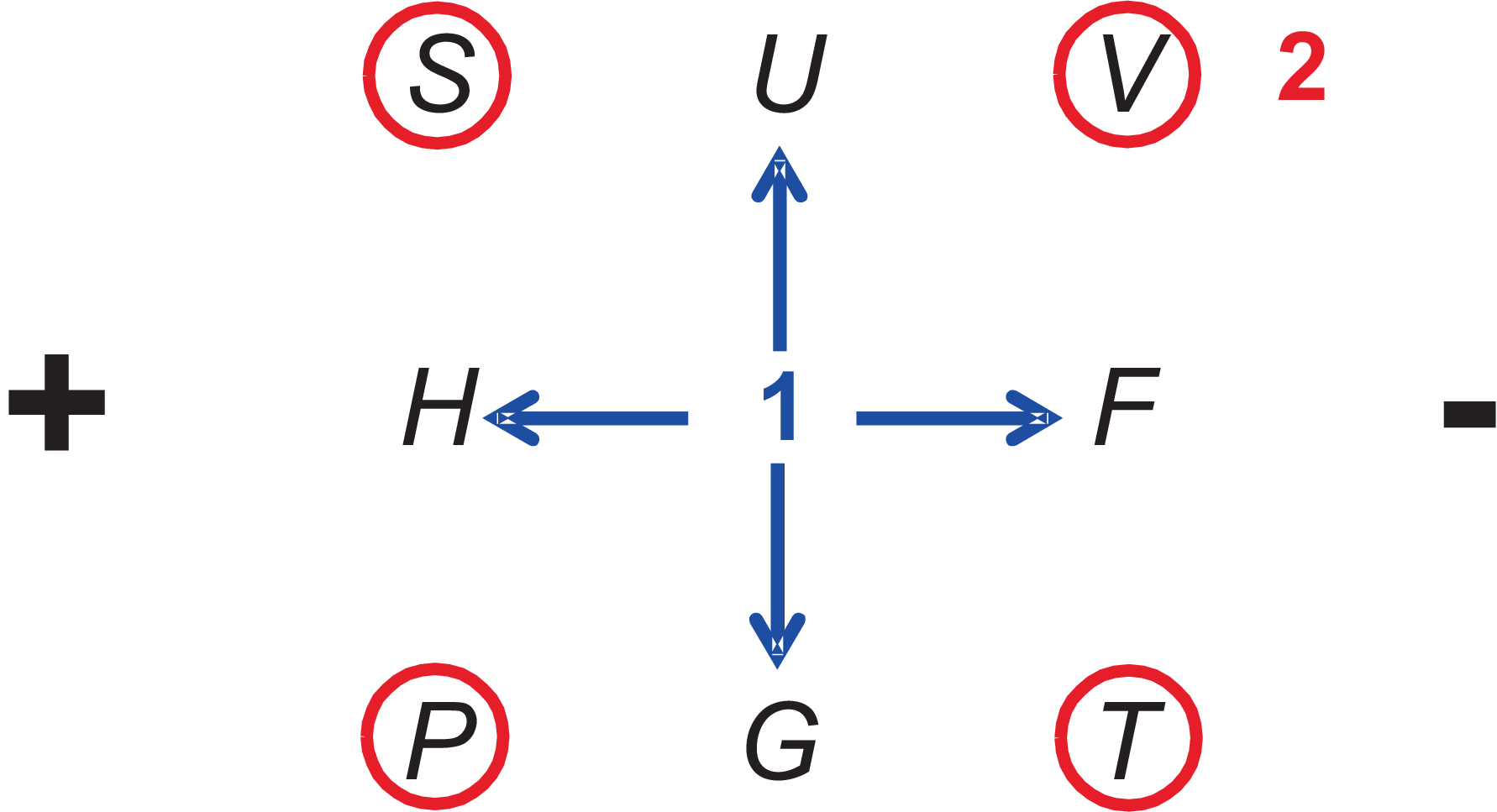
Figure 3.9:
Guggenheim scheme to memorize the parameter dependency and signs for thermodynamic potentials.
For reversible processes according to the definitions and following the rules of the Legendre transformation (and ignoring the dependence on \(N\))

we found
Differential term of \(U\), \(F\), \(H\), and \(G\) on left side of the fundamental equations. Direct neighbors are the natural parameter.
Differential terms on right side of the fundamental equations and relevant signs; associated are \(T\), \(S\) and \(p\), \(V\).
© J. Carstensen (TD Kin I)