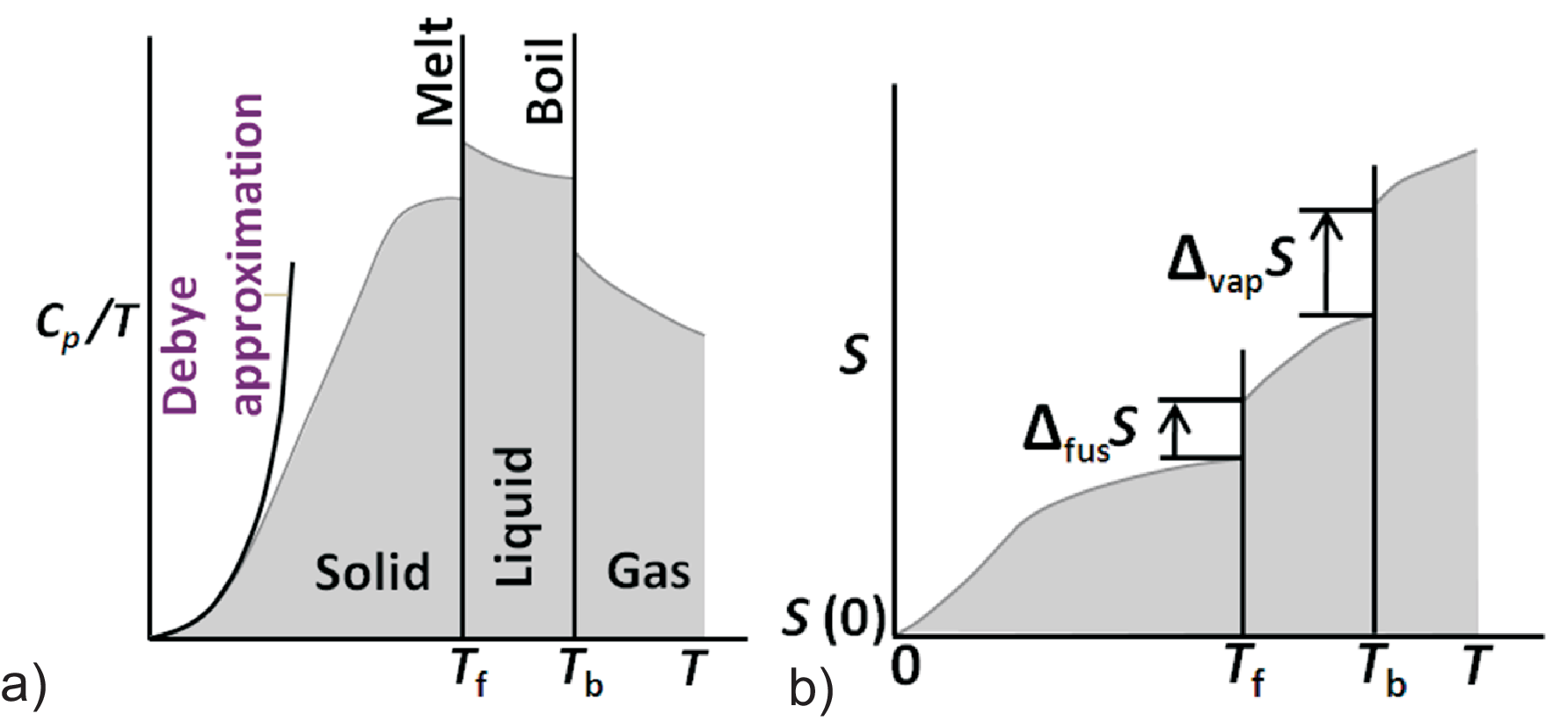
Figure 3.8:
Entropy vs. \(T\) dependence: a) \(C_p/T-T\) diagram; b) \(S-T\)
diagram.
We will now discuss the change of entropy with temperature as illustrated in Fig. 3.8 b). Thus we have to apply successively the general Eq. (3.17). For the first-order phase transitions with constant \(T_{trs}\) we already found the mathematical solution by Eq. (3.18). To perform the integration if the changes in \(dH\) are continuous and if \(T\) is not constant we apply the heat capacity.
We get
|
| \begin{equation*} S(T) = 0 + \int_0^{T_f} \frac{a T^3}{T}dT = \frac{1}{3} a \, T_f^3 = \frac{1}{3} C_p(T_f) \label{eq:S_vs_T_Debye} \end{equation*} | (3.21) |
Similarly one can describe the contribution of electrons to the heat capacity (usually assumed to be linear) leading to \(S(T) = S(0\;\mbox{K}) +C_p(T)\)
© J. Carstensen (TD Kin I)