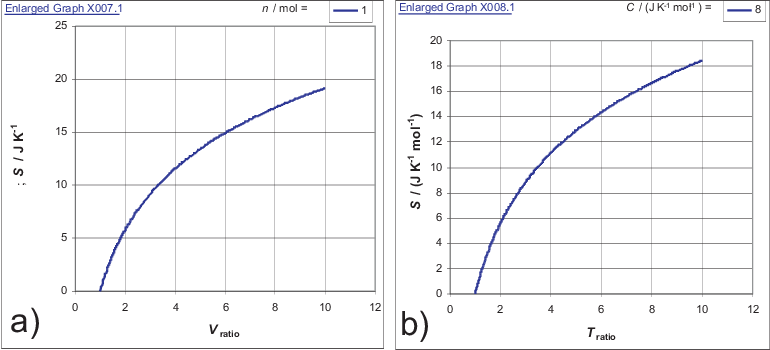
Figure 3.1:
Entropy change for a) isothermal expansion; b) isochoric change.
Here we provide some fundamental equations regarding the entropy for the expansion of a perfect gas under different boundary conditions resulting in reversible changes between an initial state \(i\) and a final srate \(f\). As stated above we use the first law to calculate \(dq_{rev}\) and finally apply Eq. (3.1) to calculation \(\Delta S\):
Isothermal expansion, i.e. \(U=3/2 \, n \, R \,T=const.\) or \(0 = dU=\delta q + \delta w\) (cf. Eq. (2.16)):
Isochoric expansion, i.e. \(\delta w = 0\), or \(C_V dT = \delta q = dU\):
|
| \begin{equation*} \Delta S = \int_i^f \frac{dq_{rev}}{T}=C_V \int_i^f \frac{dT}{T} = C_V\, \ln \frac{T_f}{T_i} \label{eq:dS_isochoric} \end{equation*} | (3.4) |
Adiabatic expansion:
|
| \begin{equation*} \Delta S = 0 \quad \mbox{since} \quad \delta q = 0 \label{eq:dS_Adiabatic} \end{equation*} | (3.5) |
Fig. 3.1 visualizes the logarithmic behavior described by Eq. (3.3) and Eq. (3.4)
© J. Carstensen (TD Kin I)