A comment on internal pressure and Joule’s experiment

2.4 A comment on internal pressure and Joule’s experiment

Here we briefly discuss the meaning of the partial derivatives in Eq. (2.8):

Figure 2.1: Joule experiment: expansion of real gas in vacuum, i.e. without change of inner energy \(U\).

\begin{equation*} dU = \left(\frac{\partial U}{\partial T} \right)_V dT + \left(\frac{\partial U}{\partial V} \right)_T dV = C_V dT + \pi_T dV \label{eq:dU_TV_2} \end{equation*}

(2.11)

\(C_V\) is called heat capacity, \(\pi_T\) is called the internal pressure. For an ideal gas the internal pressure \(\pi_T\) is zero because no energy contribution is related to the distance of the molecules, independent if this is induced by changes of the volume or the pressure:

\begin{equation*} \pi_T = \left(\frac{\partial U}{\partial V} \right)_T = 0 = \left(\frac{\partial H}{\partial p} \right)_T \label{eq:intp_0} \end{equation*}

(2.12)

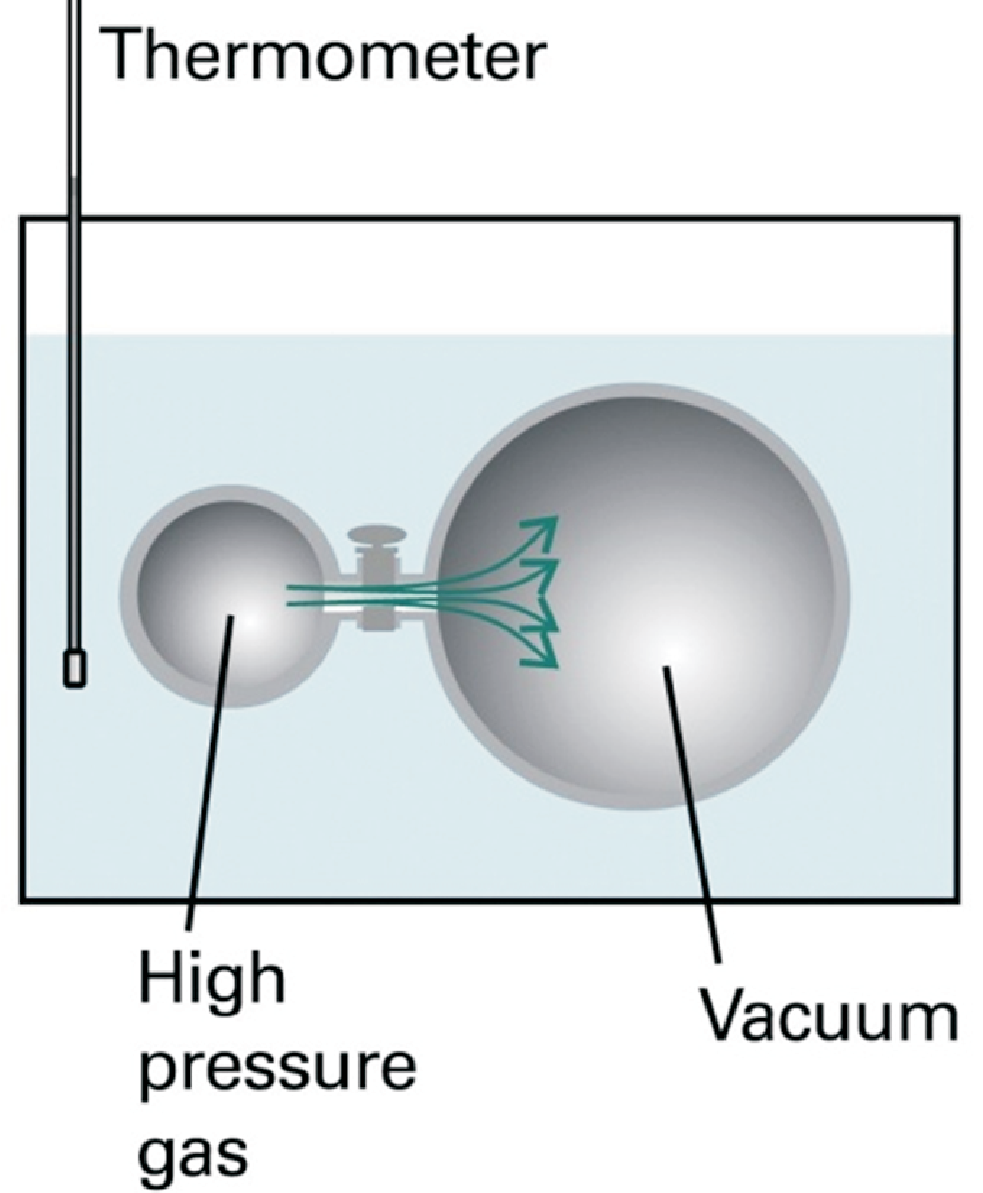
Later on we will discuss why either inner energy \(U\) or enthalpy \(H\) are needed for a calculation of the corresponding partial derivatives. The experiment Joule performed to check Eq. (2.11) is illustrated in Fig. (2.1). We have to answer several questions before we can understand all aspects of this experiment:

How do we arrange and conduct an experiment with \(dU = 0\)?
How do we measure / calculate work?
Why does a system perform no work when expanding against vacuum?
Why is \(\partial U / \partial V\) called internal pressure?
How do we measure heat energy?

First of all we need a precise definition for the heat capacity \(C\) of a body. It is by definition the ratio \(\delta q / dT\) of the amount of heat \(\delta q\) absorbed by the body to the associated infinitesimal change in temperature \(dT\). The heat capacity will in general be different if the body is heated at constant volume or at constant pressure. In order to be more precise we here need \(C_{V,N}\).
In a nutshell: In Joule’s experiment \(\delta w\) is zero. Joule found no change of temperature of the surrounding water from which he concluded that no heat has been exchanged between the system and the surrounding water. Consequently he concluded that \(\pi_T = 0\). Actually this was just a (lucky) measurement error due to the large heat capacity of the surrounding water, i.e. the small amount of heat energy \(\delta q\) lead to a negligible (not measurable) change in temperature.