Solution to Exercise 8.1-2

Optimal Working Point of Solar Cells

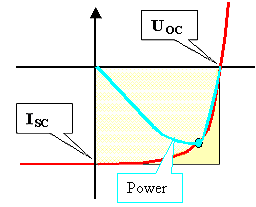
The figure shows the IV-characteristics of a real solar cell. Derive the optimal working point by simply constructing the I · U = Power curve graphically

This is easy. Power is P = U · I; as long as the current is relatively constant, the power curve is a straight line from the origin.

At U_OC the power is zero; for voltages a bit smaller it will go up sharply. All in all the power curve must look like the blue curve with the point of maximum efficiency somewhat below U_OC

What kind of load resistor would you need for this solar cell? What are the implications ?

In full sun light a (15 × 15) cm² solar cell delivers something like 5 A at 0.5 V, calling for a load resistor with R_load = 100 mW. It the current drops by a factor of 10 because of clouds, the load resistor must increase 10 fold, otherwise the voltage drops below the optimum value .

This means that not only do we have very small (and difficult to handle) load resistors, we also need an active load management if maximum power is to be harvested from solar cells with necessarily strongly changing output.

With frame

Exercise 8.1-2 Optimal Working Point of Solar Cells