Solution to Exercise 7.1-2

Forces in Capacitive Structures

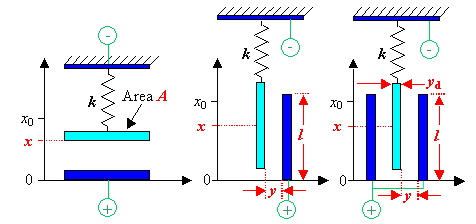
Here is the drawing once more to avoid jumping back and forth:
Capacitive forces
1. Find the proper relations for the forces pulling at the moveable plates for all three configurations.
The total energy E for all three configurations is simply given by
E  = 
ó
õ

 U · I · dt   + 
ó
õ

 k · (x – x0) · dx
With the simple relations C = Q/U, I = dQ/dt and therefore U · I · dt = (Q/C) · (dQ/dt) · dt = Q/C · dQ, we obtain
E   =  Q2
2C 		   +  k · (x – x0)2
2 
     
    =  C · U2
2 		   +  k · (x – x0)2
2 

F   = – U2
2 		  ·   dC 
dx 		   –  k · (x – x0) 
Without integration limits we cannot get proper signs (one energy term must decrease if the other one increases because we have energy conservation) - but that is not important here since we know that the spring force and the capacitive force must have opposite signs, and we are only interested in the capacitive force F C.
For the capacity C and the force F C = ½U2 · (dC/dx) we obtain:
       
1. Configuration:  
C1    =  e0 · A
x 
F 1    =  U2
2 		  ·   e0 · A 
x2 
         
2. Configuration:
x* is the (easy to calculate) plate overlap for zero voltage. But since it disappears upon differentiation, we do not need to spell it out.
C2    =  e0 · (x* – x) · h
y 
 
F2    =  U2
2 		  ·   e0 · h
y 
         
3. Configuration:
C3 is simply given by 2 C2 in parallel		  
C3    =  2C2 = 2e0 · (3l/2 – x) · h
y 
 
F3    =  2F3   =  U2   ·   e0 · h
y 
 
2. Compare the relative strength of the first and third configuration.
If we simply take the relation F1/F3 for equal distances between the plates (i.e. x = y), we obtain
F1
F3 		  =  A
y · h
Considering that y · h << A for typical structures, configuration 1 can transmit much more force than the other ones for about identical size.
 

3. Discuss the pro and cons of the two configurations for driving an actual actuator.
In configuration 1 the force decreases with the square of the distance between the plates; in the extreme case of zero distance the plates would stick together forever (in reality a fuse will blow).
The design rule is obvious: Use with extreme care!
In configuration 3 the force is independent on the position, which makes the design reasy. However, the force is relatively small.
The consequences are obvious too: This is the preferred configuration, but you need to employ many combs to achieve sufficient force.
   

With frame With frame as PDF

go to Exercise Basic 7.1-2 Capacitors and Forces

go to Exercise Basic 7.1-1Class Exercises and Quick Questions to 7.1 MEMS - Products and Developments

go to Exercise Basic 7.1-1Class Exercises and Quick Questions to 7.1 MEMS - Products and Developments

© H. Föll (Semiconductor Technology - Script)