Fermi Energy Calculation

	Lets quickly recount the essentials:
		The concentrations of electrons or holes in the conduction or valence bands are
		ne–  =  Neff · f(EC,EF,T)         nh+  =  Neff · [1  –  f(EV,EF,T)]
		The density of states for the donors and acceptors is simply their concentration ND and NA, we thus have :
	Concentration of non-ionized (neutral) donors NDo (i.e. the electron is still sitting on the donor level)
		NDo  =  ND · f(ED,EF,T)
		Concentration of ionized donors ND+ (i.e. the electron is in the conduction band).
		ND+  =  ND · [1  –  f(E,EF,T)]
		Concentration of ionized acceptors NA– (i.e. an electron from the valence band is sitting on the acceptor level):.
		NA–  =  NA · f(EA,EF,T)
		Finally, the concentration of neutral acceptors NA0; it is
		NAo  =  NA · [1  –  f(EA,EF,T)]
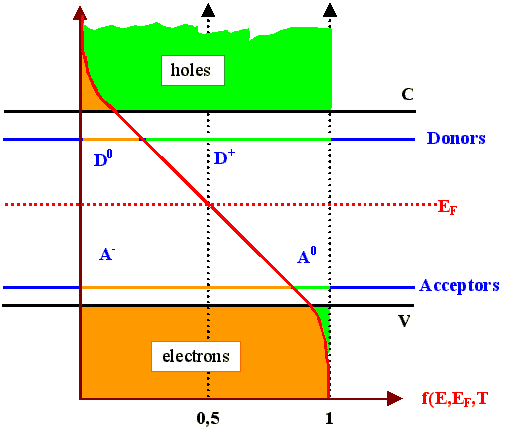
	This can be easily envisioned in a simple drawing
	The Fermi energy results from equating the sum of all negative charges with the sum of all positive charges.
		The resulting equation is easily written down, but cannot be solved analytically.
		That is why we do it numerically.

	In the following JAVA module, you can enter any (sensible) concentrations for donors and acceptors including their level in the bandgap and the temperature. The results can be displayed with adjustable axis (e.g. as Arrhenius plot with lg y over 1/x or linearly; y over x, or even as sin x over cos y if you fancy that) as a function of temperature. They include:
		The position of the Fermi energy in the band gap (only half of the gap is shown)
		The density of holes in the valence band
		The density of electrons in the conduction band.

	This calls for a little work: Note: You can enlarge any portion of a curve by simply pulling out a rectangle with the part of the curve you want enlarged in it.
		First look at intrinsic Silicon. Enter "=" for the concentration values of

With frame

2.2.2 Doping and Carrier Concentration

© H. Föll (Semiconductor - Script)