| |
 |
The chemical and electrochemical reations for pore-formation
are for all kind of pores the same. Pore growth in Silicon can be described in
most general terms (neglecting all specific dimensions and morphologies) as a
phase separation of the silicon surface into two areas: (i) the pore tips,
where all (or most) of the current is flowing; (ii) the pore walls and the
remaining silicon surface where no current is flowing, i.e. where the surface
is "passivated" against dissolution. Phase separation, in general,
can be understood as the result of the optimization of purely local phenomena
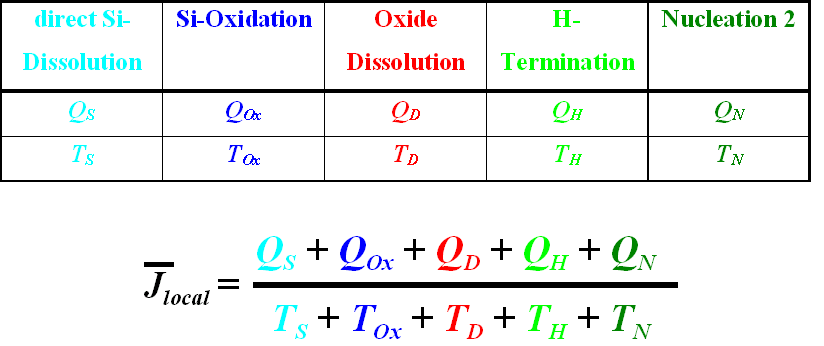
mediated by stochastic processes. We thus define a local process for the
silicon dissolution which consists of a series of charge (Qi) and time (ti)
consuming processes called "current bursts". Each local current burst
carries a mean current which has a specific optimum value for a particular
system. The average number N of current bursts on the silicon electrode for a
constant external current I is given by number of burst per area. Since each
current burst dissolves only a small area. At each pore tip we thus find the
current density j = current burst current, independent of the size of the
pores, which, as a first result, explains the "Lehmann formula".
If we increase the external current density up to J » j, the maximal
current density under pore etching conditions is reached. This point on the IV
curve is the PSL-peak, so we find JPSL » j. To understand micro-, meso-
and macropore formation, we have to explain how the local fixation of the
current density to j will simultaneously lead to the postulated phase
separation. For that we have to be more specific and we must consider the
series of processes in each current burst. This will be discussed in detail,
here we present just an outline: (i) Each current burst has to overcome an
existing H-passivation of the surface (nucleation phase); (ii) a direct
dissolution of silicon occurs; (iii) silicon may be oxidized; (iv) the silicon
oxide has to be dissolved; (v) at the clean surface a (relatively slow)
H-passivation starts. Only in ii) and iii) charge is transferred, all processes
need time. The current can be increased to its optimum value by maximizing the
consumed charge, and/or minimizing the time needed. Since the pore nucleation
is much easier on unpassivated surfaces, H-passivation is (A) a process which
can increase iB by reducing the time between the beginning of H-passivation and
pore nucleation, and (B) a mechanism which leads to a preferential pore
nucleation in areas where current bursts just stopped. This correlation in time
between two subsequent current bursts is the driving force for the phase
separation, i.e. the clustering of current bursts in some areas and thus to
(meso and macro) pore formation. The H-passivation can explain another
fundamental aspect of pore formation: The strong crystal orientation
dependence. Since the number of dangling bonds on the (100)-surface is much
higher than on the (111)-surface, the H-passivation is fastest and most
effective on (111)-surfaces. Con-sequently current bursts occur preferably on
(100)-surfaces leading - in many but not all cases - to an effective pore
growth in (100)-directions and to (111)-surfaces as preferred pore walls. The
processes (ii) to (iv) are strongly influenced by changing the oxygen
concentration in the electrolyte and the proc-esses (i), (ii) and (v) by the
concentration of hydrogen. This dependence on the chemical composition of the
electrolyte allows to control the local current density j as well as the
driving force for the phase separation. Just by "designing" the
electrolyte one can stabilize or destabilize the ability of the Si-electrode to
form pores on an extremely local scale. In addition to all the non-local
processes mentioned above which may stabilize pore growth, this chemical
component allows to increase the regime where pores of different morphologies
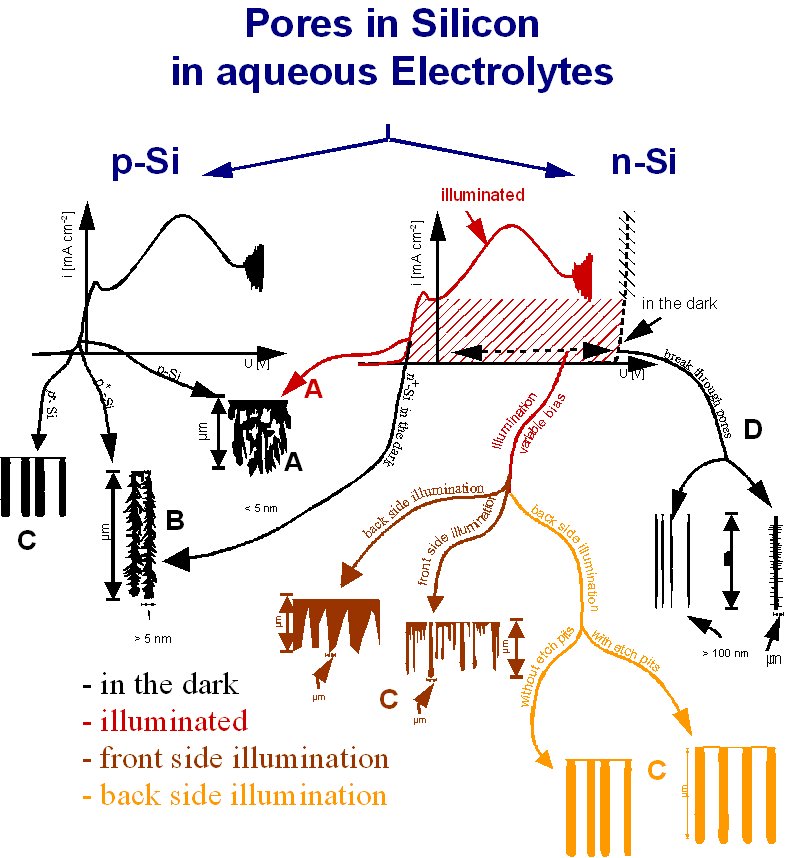
can grow stable. Conclusions: The current burst model allows for a deeper
insight into the mechanism of pore formation in the silicon HF system and
probably in other semiconductor systems as well. This allows to increase
substantially the range of sta-ble pores of different morphologies. By changing
only the chemical composition of the electrolyte, one can change e.g. from
stable mesopore- to macropore-growth and vice versa. Extremely stable
macropores can be formed, e.g. in p-Si-samples using organic electrolytes which
would not grow in aqueous electrolytes. |
|