CURRENT TRANSIENT ANALYSIS OF THE OXIDIZING PROCESS IN
THE COMPLETE ANODIC REGIME OF THE SI-HF-SYSTEM
G. Hasse, J. Carstensen, G. Popkirov, H.
Föll
Faculty of Engineering, University of Kiel, Kaiserstr. 2,
24143 Kiel, Germany
Potential step experiments from anodic potential to open circuit potential in the electrochemical system Si-HF result in a transient current peaks, provided that oxide was present at the electrode surface. The current transients can be analyzed quantitatively and provide information about the anodic oxide and the electrode processes. In this paper it is shown that the complete I-V-characteristics (including the region of PSL formation) is governed by the oxidation process, that the points of inflection (and not the maxima) indicate changes in electrode processes, and that several linear relations between electrode processes and external parameters can be obtained from evaluating the experiments. The findings are consistent with the view that the electrode processes can be seen as results of the interaction of current bursts which may be synchronized by stochastic processes in time and space and indicate in addition that simple, albeit not yet fully understood mechanisms cause the amazing multitude of phenomena occurring at the Si – liquid interface.
Silicon, Electrochemistry, I-V-characteristics, Transient measurements, Kinetics, Oxidation
Silicon in contact with HF as an electrochemical system has always been used in microelectronic technology, but has only moved into the scientific focus after it was shown that various porous layers with dimensions scaling from nanometers to micrometers can be easily obtained [1, 2]. Despite extensive research on the Si – HF system, many of its features are not fully understood. This paper investigates the oxidation process via current transient experiments at any point of the current-
|
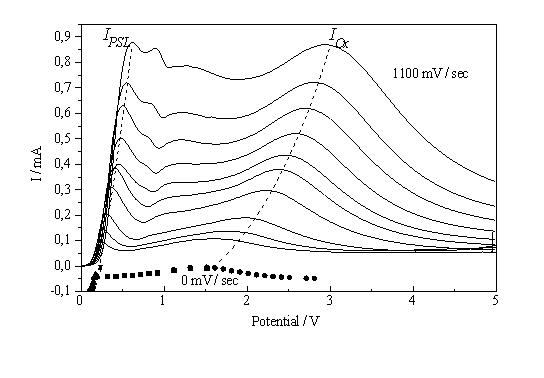
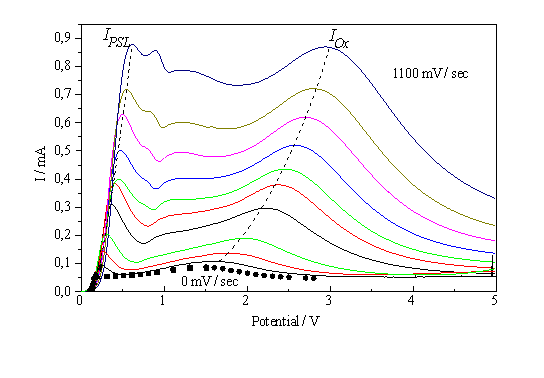
Fig. 1: I-V-characteristics of the Si – 0,05% HF system for scan rates decreasing from 1100 mV/s in approximately 100 mV steps to static conditions. The 0 mV/s data points were obtained by indirect measurements; see Fig. 3 |
voltage characteristic (see. Fig. 1), including the regions of pore formation and current/voltage oscillations, cf. [3-9].
A typical current transient experiment first keeps the Si electrode in a steady-state at a predetermined constant voltage or current which may take up to 30 min waiting time. In order to obtain current transients, the system is then switched to the open circuit voltage, which, by definition, is the voltage with zero current in the external circuit. However, if parts or all of the Si surface were covered with an oxide at the moment of the switch-over to the open circuit voltage, a current transient will be observed which contains information about the oxide present at the switching time [8-14]. In particular, the mere presence of a transient current must be seen as conclusive evidence for the presence of an oxide at least on parts of the electrode surfaces for the particular system configuration chosen for the measurement. This does not exclude the possibility that a process of H – termination, starting after the oxide has been removed, adds some charge [14], but from our experiment we feel justified in neglecting this contribution.
Details of the technique used are explained in [9]. All samples were p-type Si with a resistivity of 1-5 W cm. They were inserted into a PVC-cell and contacted by using InGa-Alloy. The electrolyte consisted of a 0.05 w% HF solution with added NH4Cl in order to reduce the electrolytes resistance.
For all measurements a custom built potentiostat or galvanostat was used, allowing for sudden voltage and current switches without signal interference by, e.g., recharging parasitic capacitors. The experimental setup employed four reference electrodes to eliminate the influence of voltage drops due to contact- and electrolyte-resistance. The signal was filtered by a Stanford SR 640 Filter. The electrolyte was cycled through the cell by a peristaltic pump and its temperature was kept constant by a Julabo thermostat.
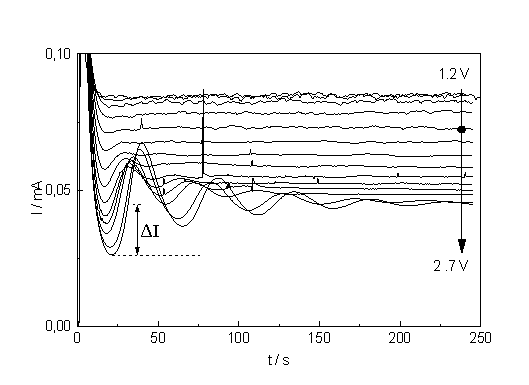
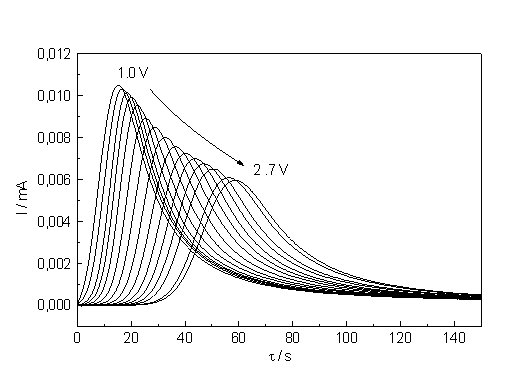
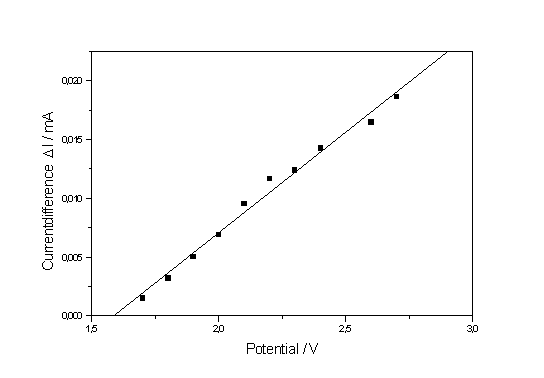
| a) b) Fig. 2: a) Current - time curves for potentials ranging from 1.2 to 2.7 V. The spot marks the curve belonging to 1.7 V. The parameter D I (see text) is a measure for the synchronization strength. b) Corresponding current transients measured at potentials ranging from 1.0 to 2.7 V. The equilibrium values of I are used to construct the static I-V-characteristics. |
At higher potentials and beyond the broader peak in the I-V-characteristic, (which will be referred to as IOx - peak) the current oscillates despite a constant cell potential [5-9]. Since oscillations are closely related to the growth and dissolution of anodic oxide [8, 9], measurements of current transients proved fruitful for the investigation of this phenomena [5, 8, 9]. In this paper, however, we focus on "equilibrium"-states, i.e. on current transients measured after the (damped) oscillations died out. The current vs. time curve is shown in Fig. 2a for voltages on the descending part of the IOx - peak. It is obvious that higher potentials improve the odds for oscillation. Following the oscillation model described in [8, 9], we assume that oscillations occur whenever "micro oscillators" are synchronized on a sizeable part of the electrode surface. The micro oscillators are localized current paths or current lines whi ch occur in current bursts [8, 9] through the oxide which are (stochastically, but periodically) turned on at high field strength (when an oxide, dissolving chemically in the HF, is thin enough), and turned off at low field strength (when the oxide grown by the current is sufficiently thick).
Synchronization may occur by a percolation process of next neighbor coupling, but may lose strength as time goes on; the oscillations then appear to be damped. An important feature of this model is that local oscillation may occur without a macroscopic manifestation – in this case only the synchronization is lacking - and that areas below an active micro oscillator do not show suboxide charge. In consequence, if a current transient is measured for an electrode state where many micro oscillators are active, the total charge as obtained by integrating the transient curve is smaller as compared to a state with few or no active oscillators.
If the current deviates from the equilibrium value, however slightly, in a current vs. time measurement, this then must be taken as an unambiguous indication of micro oscillations and of the onset of synchronization. In Fig. 2a oscillations thus begin at least at 1.7 V (the corresponding current time curve is marked by a black dot in Fig. 2a which corresponds to the point of inflection on the downward slope of the IOx – peak
|
Fig. 3: D I (as a measure of the synchronization strength) vs. potential exhibits linear behavior |
Fig. 2b shows the current transient measurements corresponding to the I-t-curves in Fig. 2a. With increasing potential the transients become lower in height and, albeit they broaden, integration shows that the area (i.e. the total suboxide charge) is increasingly reduced. This results indicate not only that micro oscillators are still present after the macro oscillations disappeared, but that their effective area is growing with increasing voltage. As a measure for the synchronization we may take the difference of the lowest current value to the equilibrium value, which is plotted in Fig. 3. From the theory given in [8, 9] one must expect that the synchronization strength increases with increasing potential (or rather mean oxide thickness). The straight line obtained in Fig. 3 is a clear indication that the synchronization process, though complicated and stochastic in nature, follows simple relation which have yet to be found in the theory of oscillati ons and that it starts around the point of inflection.
Another interesting feature is the reduced "roughness" or noise of the current - time curves (Fig. 2a) for higher potentials. If this noise is analyzed by calculating the autocorrelation function of the signal, a clear peak is found at the frequency of the oscillations, indicating that the noise is due to the formation of small domains of locally synchronized oscillators, but with random phases between domains.
An intriguing point is the onset of macroscopic oscillations at the inflection point of the I-V-characteristics. This means that when the curvature changes from negative to positive, a current supporting mechanism must start or become dominant.
A possible explanation uses the picture of small (fluctuating) domains with synchronized oscillators within a domain but with random phases between domains. If two domains are next to each other, the border area will be in an intermediate state with a relatively constant oxide thickness that does not allow the nucleation of local oscillators. This border areas are thus inactive and do not support current flow. If with increasing macroscopic synchronization more and more domains synergetically join the major synchronization beat and become phase-linked, these inactive areas decrease and the current increases. There may be other mechanisms, however, which must be considered in an advanced model of the oscillations.
Whereas this explanation may be worked out in more detail as a mechanism that agrees well with the current model of oscillations, the coupling of current to border area size does only apply to oxidizing currents. Since the total current must be seen as the sum of an oxidizing current IOx and a non-oxidizing INox (which most likely leads to direct Si dissolution) it is necessary to know the relative magnitude of each current in order to fully understand the electrode behavior.
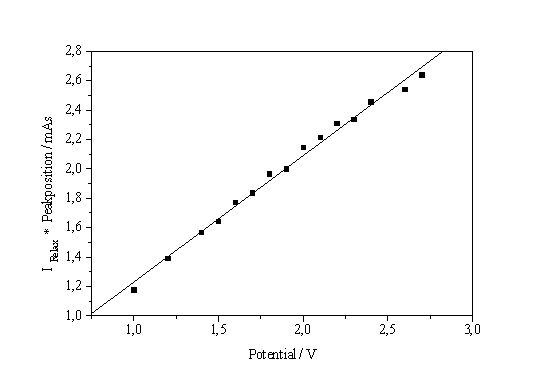
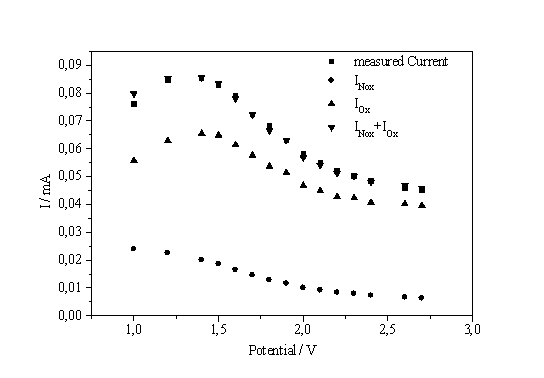
| a) b) Fig. 4: a) Current on the I-V-characteristic times peak position vs. potential. b) Current split into oxidizing and non-oxidizing part |
So far, no information about the splitting of the total current I in IOx and INox was reported. A possible way to obtain this relationship by analyzing current transients is shown in Fig. 4a. The current of the I-V-characteristic at a given potential multiplied by the position of the corresponding transient peak maximum on the time scale (which is proportional to the oxide thickness) is plotted versus the potential and results in a rather perfect straight line. This observation can be expressed as follows:
![]() (1)
(1)
with A and B describing the y-axis offset and the slope of the measured line. And the current I divided into I = IOx + INox.
The linear increase of It now is mainly due to the increase in t , which in turn mirrors the increase in mean oxide thickness d. It is now sensible to assume that non-oxidizing currents decrease with increasing d; we use for the sake of simplicity a 1/d relationship. Then the constant parameter A can be identified as the term INoxt . While t increases with the potential INox decreases. Consequently, IOxt and BU must be equivalent. We thus obtain in the most straightforward approach:
![]() and
and
![]() . (4)
. (4)
The result of this analysis is shown in Fig. 4b. The IOx part of the current is always dominating – including the low voltage regime to the left of the IOx - peak - and it determines the form of the characteristics.
Without going into details, we conclude that the results are fully compatible with the oscillation model given in [8, 9], but provide new insights that can be used to improve the model. In particular, it appears that the point of inflection on the upward slope of the IOx - peak marks first complete coverage of the electrode with oxide (which is a necessary condition for the analysis given above), that the current increase after this point is due to an enhanced dissolution rate of the oxide caused by the rapid increase in oxide roughness (see Eqn. 2 in [9]) after the inflection point, and that the electrode to the left of the inflection point is covered with (ever changing) oxide islands next to patches of a (H – passivated) Si surface. The formation of first small domains with synchronized micro
|
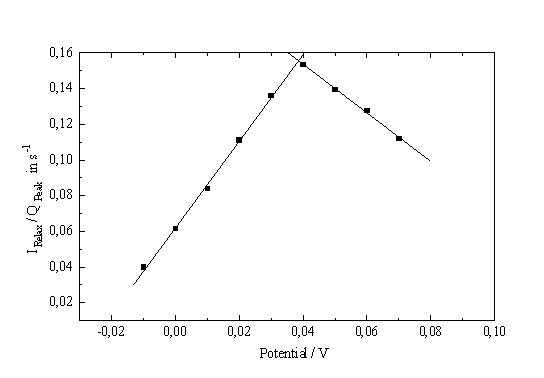
Fig. 5: (Current / Charge in transient current peak) vs. potential |
oscillators after the first inflection point counteracts the current increase by decreasing the roughness, the growth of the domains, causing increasing noise, counteracts it even more, because now increasingly inactive domain boundaries are formed. The IOx - peak thus signifies the equivalence of the current increasing and decreasing factors. At the second inflection point the fully developed domains with maximum boundary area start to coalesce into large domains which cover sizeable parts of the electrode surface and exhibit macroscopic oscillations.
Transient current experiments were performed for the first time in this area of the I-V-characteristics, again after a sufficient waiting time for equilibrium conditions. Transients were clearly observable, which may be seen as relatively direct proof of the existence of oxide in this region. An integration of these peaks shows that the suboxide charge grows with increasing potential. This can be attributed to increasing area coverage of silicon with oxide.
Lack of space requires to show only the most significant result; it is obtained by plotting the ratio of the (equilibrium) current and the total charge contained in the corresponding current transient vs. applied potential. Fig. 5 shows that this procedure results in two straight lines of different slopes, which intersect at the point of inflection of the I-V-characteristic in the ascending region of the PSL-peak.
Tentatively we identify this point with the first occurrence of oxide islands. This means that starting at the inflection point the oxide (or rather the chemical dissolution of the oxide) starts to dominate the I-V- characteristics). This does not preclude that oxide forming electrochemical reactions occur before this point; it only means that the oxide dissolution process is "faster" than the generation process. Again, the average oxide thickness in the oxide patches is of paramount importance for the interpretation of the I-V-characteristic.
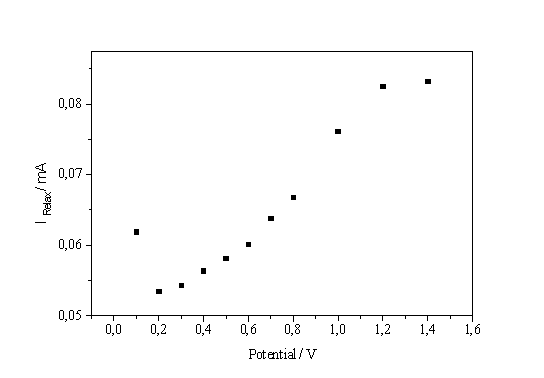 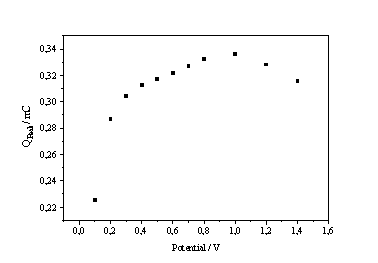
Fig. 6: a) Current on I-V-characteristic in static conditions b) Transient charge vs. potential in the electropolishing regime |
Analogous experiments done in the electropolishing regime of the characteristics (i.e. currents between IPSL and IOx) provide the link between the PSL-regime and the oscillations. The curve that shall be presented here is the transient charge versus the potential (Fig. 6b). The increasing charge represents the continuing oxide coverage which is obviously complete at the maximum of the curve in Fig. 6b, which, in total accordance with the model presented, corresponds exactly to the inflection point of the I-V-characteristics (cf. Fig. 6a). Beyond this point increasing number of micro oscillators (carrying no charge for transients) reduce the amount of observable charge. The oxide coverage, however, is not reduced.
Non oxidizing currents, which, according to Fig. 4b, are still present, either flow through the open channels of the micro oscillators or are tunnel currents through the oxide.
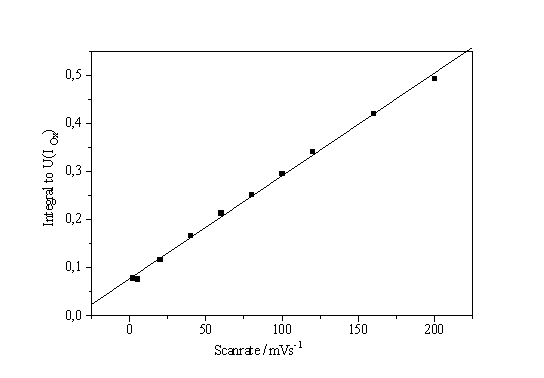
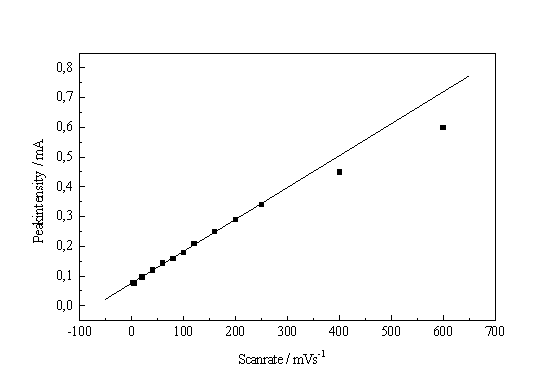
When measuring the I-V-characteristic of a system that is very dependent on slow chemical reactions, the scan rate is of great importance for the interpretation of the experiments. As shown in Fig. 1, even scan rates smaller than 100 mV/s may distort the characteristics, at larger scan rates even new peaks may occur. The scan rate dependence of the characteristics, however, may also be used to obtain information concerning kinetic processes of the system. If we plot the height of the IOx - peak vs. scan rate, an approximately linear curve is obtained (Fig. 7a).
The straight line in Fig. 7 a, if analyzed in the context of the theory given in [8, 9], demands in a first approximation that the field strength is always constant, which in turn demands that the mean oxide thickness is always proportional to the applied potential.
Fig. 7b. shows another way of evaluating the influence of the scan rate on systems kinetics. Here an integration of the characteristic from 0 V to the (scan rate dependent) potential of the IOx - peak was made and plotted versus the scan rate. Again a linear curve results, which is easily analyzed. Neglecting the y-axis offset we write:
| a)
Fig. 7: a) Height of the IOx – peak vs. scan rate. b) Integral of the characteristic from 0V to the IOx potential vs. scan rate. |
 (9)
(9)
Replacing dU by vgdt results in
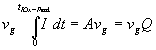 (10)
(10)
with Q = total charge consumed to arrive at the IOx - peak.
This means the parameter A can be identified as the charge Q, that was needed to built up the oxide at the IOx - peak and that this charge is constant for all scan rates! This is in accordance with the interpretation of Fig. 7a: Faster scan rates require larger currents to maintain the proper oxide thickness. In consequence, supporting and surmounting everything said before, it becomes clear again that the oxidation process determines the I-V-characteristics.
[2] V. Lehmann, U. Gösele, Appl. Phys. Lett., 58,(1991) 856
[3] H. Föll, Appl. Phys. A 53,(1991) 8
[4] R.L. Smith, S.D. Collins, J. Appl. Phys. 71 (8) (1992)
[5] F. Ozanam, N. Blanchard, J.-N. Chazalviel, Electrochimica Acta, 38 (12),(1993) 1627
[6] J.-N. Chazalviel, C. da Fonesca, F. Ozanam, J. Electrochem. Soc., 145, (3) (1998) 964
[7] S. Cattarin, J.-N. Chazalviel, C. da Fonseca, F. Ozanam, L.M. Peter, G. Schlichthörl, J. Stumper, J. Electrochem. Soc., 145, (2) (1998) 498
[8] J. Carstensen, R. Prange, H. Föll, J. Electrochem. Soc., 146 (3),(1999) 1134
[9] J. Carstensen, R. Prange, G.S. Popkirov, H. Föll, Appl. Phys. A 67, (1998) 459
[10] C. Serre, S. Barret, R. Herino, J. Electrochem. Soc. 141 (8), (1994) 2049
[11] M. Matsumura, S. R. Morison, J. Electroanal. Chem. 147, (1983) 157
[12] H. Gerischer, M. Lübke, Ber. Bunsenges. Phys. Chem. 92, (1988) 573
[13] F. Ozanam, J. N. Chazalviel, A. Radi, M. Etman, Ber. Bunsenges. Phys. Chem., 95 (1), (1991) 98
[14] J. Rappich, H.J. Lewerenz, J. Electrochem. Soc., 142 (4), (1995) 1233
 b)
b)