A Stochastic Model for Current Oscillations in Space
and Time at the Silicon Electrode
H. Föll, J. Carstensen, M. Christophersen, G.
Hasse
Faculty of Engineering, University of Kiel
Kaiserstr. 2, 24143 Kiel, Germany
The "current burst" model, originally developed for current oscillations at the Si electrode, is generalized and applied to all phenomena encountered in Si electrochemistry. The essential assumptions of the model are: 1. Current flow is inhomogeneous in space and time; it occurs in current bursts; and 2. Current bursts interact, inducing oscillations of the current in time and space (=pores). It is shown that many phenomena can be understood for the first time with this model and that detailed predictions are possible allowing to test the model. |
INTRODUCTION
Research of the anodic dissolution of silicon in Fluorine containing electrolytes yields an increasing number of phenomena which may be most generally characterized as current oscillations in time and space. Oscillations in time comprise not only stable current (or voltage) oscillations at constant voltage (or current, respectively) (1-3) but also damped current oscillations and oscillations hidden in noise (4). Current oscillations in space are better known as pits or pores, and it is the large variety of pores obtainable in Si by probing the available parameter space together with the potential for novel products that finds increasing interest in the scientific community. Pore geometry's and morphologies comprise sponge-like structures in the nanometer range (generally addressed as micropores), mesopores in the 2 nm – 50 nm range always following <100> directions, "well-formed" macropores in the micrometer range - straight, smooth, and with aspect ratios of 500 and larger - heavily branched macropores with rather peculiar morphologies, and two-dimensional structures termed "trenches" and "wings". In addition, the dependence of the pore morphology on crystal orientation shows peculiar effects, e.g. pore growth directions in <113>. Fig. 1 gives a taste of the variety encountered in pore etching; details (and references) can be found in the more recent reviews and papers (5-7).
 |
 |
 |
 |
 |
 |
| Fig. 1: Macropores obtained under comparable conditions: a) Current modulated (sine wave, f=33 mHz, 20% amplitude) n-type Si, 9 Wcm, back side illuminated, DMF + 4% HF; b) as a), but no current modulation; c) as b) but p-type Si; d) p-type Si, 10-20 Wcm, H2O + 7% HF, pre-structured nucleation, top view; e) as d), cross-section; f) as e), but random nucleation. | ||
Many attempts have been made to understand the dissolution process and the mechanisms responsible for its apparent instability in space and time. While much progress has been made in recent years, much remains mysterious and there is a general lack of predictive power, cf. the newest papers on this subject (6). Moreover, a whole new world of electrochemically formed pores emerges in other semiconductors with many similarities to Si (8), but also many differences and most likely a wealth of phenomena not yet discovered, cf., e.g., (9).
It appears to be an over ambitious and hopeless goal to understand these and other phenomena from just a few basic principles – and that may well be the realistic of view of the subject. Nevertheless, it has not been proven that this goal can not be reached, and in this paper, based on previous work (10, 11), an unified approach to Si electrochemistry is attempted under the heading "current burst model" (CBM) which at present must be necessarily speculative for many (but not all) facets of Si electrochemistry.
THE ESSENTIALS OF THE CURRENT BURST MODEL
The current burst model is based on the following major assumptions which will be made more specific later on:
Current flow through the Si electrode is inhomogeneous in time and space - it occurs in "current bursts" (CB). This means that charge transfer at some point r on the surface occurs for some (short) time span D tC in a small area (roughly 1 nm2) around r. The next current burst occurring within D r will be delayed by some waiting time D tw. During the time of charge transfer chemical reactions of the Si occur; these are essentially direct dissolution and oxidation. During the waiting time other chemical reactions occur, essentially oxide dissolution and hydrogen passivation of the free Si surface.
- Current bursts have an intrinsically stochastic nature. The nucleation of the charge transfer process and the two time constants D tC and D tw are not fixed values but are given by some distribution function which is determined by the system parameters. Nevertheless, the total average duration of a current burst defines an intrinsic time constant t CB =D tC + D tw of the electrochemical system which should express itself in the dynamics of the system.
- Current bursts may interact in space and/or time. This means that the nucleation probability and/or the individual properties of a CB at r and t may depend on the state of current bursts at r + D r (interaction in space) or at t - D t (interaction in time).
While these assumptions project a radical departure form conventional views of the (homogeneous) electrode processes, it is obvious that the three basic chemical processes at the electrode – direct dissolution, oxidation and oxide dissolution – can not all occur at the same time and space - the electrode state thus must be inhomogeneous at some scale by necessity. The CBM essentially exploits this point by specifying the sequence of reactions as a current burst and the resulting electrode state by the interaction of current bursts.
CURRENT OSCILLATIONS AND THE CURRENT BURST MODEL
The current burst model was originally developed to model the current oscillations occurring at higher potentials. In this case, the CBM can be simplified: nucleation of CBs always occurs through an oxide layer; the nucleation probability (begin of charge transfer) as well as the quenching probability (end of charge transfer) depends only on the field strength in the oxide (i.e. on the local oxide thickness) and the only chemical reactions are oxidation (during charge transfer) and oxide dissolution (during the waiting or quiescent period). The average current ICB flowing in a current burst then is I CB =Qox/(tox + tod) with tox=average time for charge transfer, tod=average time of oxide dissolution, and tod << tox in most cases. For simplicity the adjective "average" will be omitted from now on.
Charge consuming reactions and time consuming reactions thus may be decoupled; if tox is negligible compared to tod, the intrinsic time constant t CB is determined by the oxide dissolution kinetics only and becomes a simple function of the HF concentration.
A current burst is already a local oscillator – current on/current off conditions will occur with a fixed (average, of course) frequency. It is apparent that macroscopic current oscillations will be observed if there is some synchronization between individual current bursts, i.e. if current bursts on different points on the electrode are correlated in time. For a rigid correlation (all CBs starting and ending at the same time), current flow would manifest itself in strong current pulses with a short duration, a frequency f=1/t CB, and zero current in between. For a stochastic correlation (i.e. the likelihood for nucleation/quenching at r is modified by the state of CBs in the immediate neighborhood) "wavy" I(t) curves may result and the current may never be zero – but the frequency is still approximately determined by 1/t CB and thus by the oxide dissolution kinetics in a direct way. If the correlation is confined to an area smaller than the electrode surface, i.e. if there are domains with a certain correlation of the CBs in the domains, but with no correlation between domains, a "noisy" current results with the noise amplitude proportional to (Lco/L)k (L=linear dimension of the specimen; Lco=linear dimension of the domain or correlation length, k=0.5 ...1 depending on the model) and a strong peak around 1/t CB in the power spectrum of the current noise (12)
The CBM in this very general form not only accounts naturally for oscillations in time per se, but makes rather detailed predictions about current oscillations and related phenomena. The crucial questions still open are:
- What kind of next neighbor interaction leads to a correlation in time of the affected CBs?
- How does this interaction spread leading to correlated large areas (the domains)?
- What factors determines the domain size or correlation length Lco?
Ref. (3) deals with the first two questions in detail and demonstrates by quantitative Monte Carlo simulations that all properties of current oscillations as measured by many research groups can be reproduced, e.g. the concomitant oscillations of the oxide thickness, oxide roughness, capacitance or dielectric constant for a certain region of parameter space. The local interaction in space suggested in (3) stems from the lateral spread of the oxide produced during the charge transfer period as illustrated in Fig. 2 in (2). In short, a current burst nucleating between the "oxide bumps" of slightly older CBs will have to produce less oxide before it quenches because it "uses" some of the oxide of the others, which in turn decreases tod and thus correlates the end of the CB to its neighbors. While this may not be the only interaction mechanism, it is unavoidable and always present.
 |
| Fig 2: Macropore tip of a pre-structured macropore on p-type silicon (enlargement of Fig. 1e). The "hammers" are directly visible. |
The third question is not yet answered, but several independent measurements suggest that the coupling strength, as an indirect measure of the domain size, increases monotonically with the voltage (13). Without direct coupling, i.e. if the distance between current bursts were to be larger than the lateral dimension of a CB (i.e. at low CB density or smaller size of CBs), an interaction still occurs, but only randomly for some CBs. Small domains are formed in a sea of uncorrelated CBs which are "born", "die" and occur somewhere else again. In other words, the correlation length is small, phases between domains are random, and domains appear at random somewhere on the electrode (they have no "phase memory"). Between the extremes of zero or only random correlation and strong correlation over large distances, is a continuum of increasing correlation length, "phase memory", and stationarity of the domains. At some point a percolation point is reached which means that the correlation length increases to infinity. Invoking percolation theory thus appears to be a natural approach to oscillations and related phenomena.
If the domain size is considerably smaller than the specimen size, the sum of all oscillating domains will give a constant if noisy current. However, if all domains are started at the same time – e.g. by switching to some potential somewhat smaller than the potential for stable external oscillations - damped oscillations should be observed which decay with the time constant representing the "phase memory" of individual domains. This is indeed observed (13) and serves to show that besides t CB a second time constant exists: t P, representing the "phase memory" of domains. t P is tied to the domain size, it can be considerably larger than t CB (for macroscopic oscillations, with L approaching infinity, t P would become very large, too).
From this considerations it can be confidently predicted that the response to small and periodic external disturbances of the system at potentials smaller than the potentials needed for stable external oscillations (e.g. by modulating the voltage) should not only show a resonance at the internal oscillation frequency, i.e. around 1/t CB, but that the response should be strongly non-linear, i.e. contain frequencies not contained in the external disturbance signal and decay with t P. This has been observed recently by G. Hasse et al (13); Fig. 3 shows a typical response spectrum.
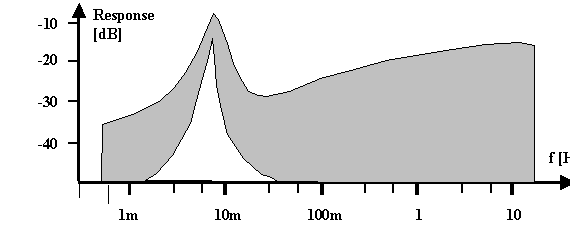 |
| Fig. 3 Schematic drawing of the general response of the current to a disturbance signal composed of 30 individual frequencies with identical amplitudes. The envelope of the linear response is shown in gray, the non-linear response in white. Both spectra show a strong peak (note the log scale) at the expected frequency of » 10 mHz. |
In conclusion, the current burst model appears to be able to explain externally observed current oscillations at higher potentials (as well as voltage oscillations, cf. (13)) and oscillating properties of the system at lower potentials. Where does its applicability end? There is no compelling reason why it should not be valid at all potentials (and, in the case of n-type Si, at all combinations of current and potential accessible by illuminating the sample). To check this hypothesis, the CBM must be made more general and more specific, and then used to predict new phenomena – especially with respect to pore formation. This will be the subject of the remainder of this paper.
GENERALIZATION OF THE CURRENT BURST MODEL
A general current burst transfers some charge Qd that leads to direct dissolution (with a valence typically around 2) and some charge Qox leading to oxidation of Si (with a valence of always 4). Within a current burst, direct dissolution must proceed oxidation because the oxide formation effectively terminates the CB. Neglecting some possible overlap, the times td and tox define the duration of the respective charge transfers.
After charge transfer (and thus the Si consuming reactions) has stopped, dissolution of the oxide takes place for some time tod. This is one of the decisive parameters of the system because the rates of oxide production and dissolution must always be equal – on average. The dissolution rate is essentially given by the HF concentration (and, of course, temperature, oxide roughness, pH-value, etc.). While in the case of the current oscillations, new current bursts always nucleated before the oxide was completely dissolved, this is not necessary in general (and unlikely at smaller voltages) – CBs may nucleate on an oxide free surface, too, but still some kind of barrier is needed that is overcome stochastically.
If complete oxide removal is achieved, in most electrolytes the free Si surface will be covered with hydrogen after some time has elapsed. The kinetics of this process depend largely on the "availability" of hydrogen – i.e. on the type of electrolyte used – and the surface type (and the temperature etc.). Generally, hydrogenation is an anisotropic process; it is always fast on {111} and slow on {100} (11). Hydrogen coverage changes not only the chemical state of the Si surface, but also the electronic state by hydrogen passivation. While a newly etched surface may have a large density of surface states in the band gap, expressed in a large surface (or interface) recombination velocity and a pinning of the Fermi level (i.e. no pronounced space charge regions can develop in the Si), H-passivation reduces the density of surface states to small numbers (14). It is important to note that the kinetics of H-passivation are not necessarily identical to those of H-coverage and in the following only the passivation kinetics are addressed. With increasing H-passivation the Fermi energy moves, a space charge region develops, field strength in the Si and the potential at the interface decreases. Since potential and field strength drive the electrochemical reactions, the nucleation probability for a current burst will decrease. However, since the average number of current bursts must be constant for constant external current, CBs must nucleate after some time tH of H-passivation, and they will do this preferentially on crystal surfaces with the least amount of passivation – always the {100} surfaces everything else being equal.
The anisotropy of hydrogen passivation thus is the major factor responsible for the anisotropy of Si electrochemistry within the CBM; it moreover provides the aging effect generally needed for many aspects of Si electrochemistry; e.g. the passivation of pore side walls. While Si (electro)chemistry is full of anisotropic processes – purely chemical dissolution of Si in, e.g., KOH, is extremely anisotropic - recent research tends to explain this anisotropy in terms of H-passivation, too (15). Immediate predictions are that pores grow preferentially in <100> directions (which is observed), and, since the second preferred direction of pore growth is <113> (11, 16), that {113} surfaces have the second slowest H-passivation kinetics (not yet determined experimentally). It is also clear that "old" surfaces (i.e. surfaces without current flow for some time and thus completely H-passivated) will remain passive - current bursts nucleate as long as the current impressed on the system can flow somewhere else – e.g. at the pore tips.
The basic equation describing a single current burst now can be written as
ICB = (Qd + Qox)/( td + tox + tod + tH) = (Qd + Qox)/ t CB [1] |
The first conclusion that can be drawn from Eq. [1] is that the current density in a current burst, jCB = ICB/FCB, is not necessarily identical to the external current density jex since the quantities in Eq. [1] depend on the system configuration in general. This means that the active area Aa = nCB . ACB (nCB =number of CBs on the electrode area A) covered by CBs may be smaller than the electrode area leading to the relation
jex / jCB = A / Aa. [2] |
Considering now the interaction between CBs just for their nucleation in a more generalized form, there are three basic possibilities:
No interaction, i.e. the nucleation probability of a CB at (r, t) does not depend on the system state at (r + D r, t - D t). Since there are many possible mechanisms of interactions this is rather unlikely. This case, however, if averaged slightly, would correspond to a homogeneous current flow as in conventional interface models.
Positive interaction in time or space; i.e. CBs have a higher probability of nucleation in areas where other CBs exist or existed. This kind of interaction acts like an attractor and favors clustering of CBs in time or space producing current oscillations or (macro)pores. The interaction of current bursts in space by their oxides as described above gives an example of a positive interaction in space. The interaction in time mediated by the H-passivation provides another positive mechanism: The likelihood for CB nucleation is low on "old" surfaces and high on fresh surfaces, i.e. in areas where other CBs expired not too long ago. This positive interaction in time would tend to induce a clustering of current bursts in some areas, while no current burst and thus no current occurs in other areas if the external current density is smaller than the current density in a CB. The result of this domain formation may be pores (if the domains stay stationary), occurring after some reorganization of the CBs if no predefined nucleation was used.
Negative interaction, akin to a repulsion between CBs. This may happen for extreme current densities (= high CB densities), e.g. when the electrode surface is completely covered with CBs, most of which are necessarily in the phase of dissolving oxide. Free areas on the electrode for the nucleation of new CBs are rare and new CBs will immediately nucleate as soon as a free spot comes up (tH assumes its minimum value of zero). This means that CBs nucleate in areas where no CBs have been nucleated for the longest possible time under those circumstances, i.e. CBs will now nucleate anti-correlated in time.
Other cases may be constructed, but it is clear that the possibilities inherent in the CBM generally allow for many effects as observed. Of course, mixed cases are likely: Current bursts cluster by the interaction in time and then form a domain by interaction in space.
For the anti-correlation case, the anisotropy behavior is mostly lost - electropolishing or micropores result. In the latter case each micropore is started by a single CB trying to avoid its neighbors. Next, quantum wire effects prevent carrier transport between fledgling micropores and essentially passivate the micropore walls formed. The resulting porous structure generates a large effective surface for dissolving the oxide of each current burst and since the oxide dissolution is always the current limiting process, anti correlation coupled with porous silicon formation allows for a current density across the electrode considerably larger compared to correlated CBs in domains and cause the PSL peak in the IV-curve. As soon as the maximum porosity is reached (all the remaining Si forms quantum wires), the system collapses to electropolishing.
So far, on a very general base, the CB model predicts pore formation as a natural phenomenon, quite independent of the system parameters. Well-formed macropores in p-type Si, e.g., are no more surprising than in n-type Si illuminated from the back. It also predicts a more or less pronounced nucleation phase for macropores because CB clustering is a kinetic process needing time. On the contrary, the often astonishing ease for nucleating macropores at pre-structured nuclei simply reflects domain pinning: Formation of pores requires not only the formation of cluster or domains of CBs, but also that they remain in place during the nucleation phase for at least the time needed to passivate the emerging side walls to a depth comparable to the correlation length. After that, the domain is caught or pinned in its own well and must dig deeper instead of moving laterally. Domain definition and pinning by pre-structured nuclei thus will produce macropores with ease in cases where random nucleation is very difficult, e.g. in p-type Si aqueous electrolytes and low current densities. Fig. 1d) and Fig. 1f), comparing random and pre-structured nucleation, illustrates this point.
Furthermore, "Lehmanns law" (17) automatically results, the only quantitative formula applicable to macropore formation (however, only within a rather small area in parameter space). It states that the ratio of the average diameter of macropores and their average distance equals jex/jPSL with jPSL = current density at the so-called PSL peak. If we identify jCB = jPSL which is quite natural as shown in (18), it is stated in Eq. [2]. Moreover and of prime importance, Eq. [1] naturally encodes complex dynamic behavior, especially for dI/dU and dI/dt, since all primary quantities involved may have specific and independent voltage or time dependencies.
So far, however, no direct statement concerning the size and morphology of pores has been derived from the CBM. Considering Fig. 1 and the extremely varied range of pores shapes reported, this is a complex issue far from being clear at present and shall only be addressed in a basic way. The essential question is what determines the specific length scales of the system under investigation which express themselves in the geometry and morphology of pores. The most advanced models for pore formation essentially define those scales, the most important ones being:
- Width of the space charge region (LSC). This was first proposed as the major parameter governing macropore formation, geometry and morphology by Lehmann and Föll (19) and has been used with great success to produce beautiful pore structures for many application. While LSC and other effects due to the space charge region undoubtedly are very important for pore parameters, it has become obvious that LSC is not sufficient to explain pores in general (20).
- Pore tip radius LAV inducing avalanche break-through. At high field strength at pore tips with a sufficiently small radius, avalanche break-through necessarily occurs, supplying plenty of carriers to drive the electrochemical reactions – a process important and often exploited in p-type Si where holes are scarce. While not a new idea (21), Lehmann et al. give a fully quantitative treatment and apply this effect to pore formation in general (22). Within the CBM model, avalanche break-through is seen as a self stopping process because small amounts of oxidation would always quench avalanche effects by decreasing the field strength. LAV thus will give the smallest dimensions possible for pores. In addition, the avoidance of avalanche break-through will lead to round pore tips having a constant field strength at any point.
- Diffusion instabilities may induce gradients in the hole concentration with a typical dimension LDif and thus induce or stabilize pores with that dimension. This case was treated in detail in (23, 24) but since LDif is always tied to the diffusion length or Debye length of the holes, LDif is too restricted to account for all effects.
- Quantum wire effects at length scales below LQu » 5 nm which prevents the movement of holes to the interface. This effect was invoked to explain the formation of micropores (25). However, while LQu indeed defines the minimum distance between micropores in the CBM too, it has nothing to say about the diameter of micropores itself.
- Another typical length, often overlooked, is the spacing LNu between lithographically defined nuclei which is totally independent of system parameters. Fig. 1d) and e) gives an example.
- The CBM finally defines a typical length too: The correlation length LCo of the interaction which defines the domain size of CBs acting in a synchronized way.
For ease of reference the correlation length will be called the internal or intrinsic length sale, the others external or extrinsic. The pores observed under certain condition result from combinations of all these length scales; it is not immediately clear, however, which one will be dominant. It is helpful to consider a graphic, if oversimplified analogy: Pores are dug into the Si with a "hammer" (mostly just one) having a size given by the intrinsic length LCo; banging away with the frequency 1/t CB. Space charge region and diffusion gradient effects essentially determine the hole concentrations on their lengths scales, they will decrease or increase the nucleation of current bursts for "wrong" or "right" geometry's and directions, and thus define the basic dimensions of macropores, while avalanche effects give the minimum dimensions. In other words, extrinsic length scales make the Si "harder" or "softer" for the CB hammer.
Three basic cases are now possible: The pore diameter, as determined by the extrinsic length scales, is 1.) smaller, 2.) larger or 3.) about equal compared to the intrinsic length scale or hammer size. The consequences are simple: In the first case, pore growth can not be sustained – one can not make small holes with a big hammer. If pores are nucleated with a spacing too small for the prevailing conditions, which would necessitate very small pores according to Eq. [2], some pores will stop growing and the others will increase their diameters as observed in many cases (20), cf. also Fig. 4a). But this explains also why it is very difficult or impossible to produce thin pores even at large induced spacings. If the second case is induced by pre-structured nucleation, the overly large length scale impressed on the system can only be adopted if more than one domain will exist in a pore - several hammers bang away independently and pores with rough side walls and a tendency towards branching will result (with a roughness wavelength directly given by the correlation length), again in perfect agreement with experiments: Fig. 2 shows the tip of the macropores shown in Fig 1e) – the individual domains are directly visible and their size corresponds to the diameter of the randomly nucleated pores in Fig. 1f). There is no pore roughness because the smallest possible distance has been assumed (cf. Fig. 1d). Fig. 4, finally shows some results of an experiment with variable spacing of nuclei and resistivity: While small spacings are not sustainable on 40 W cm material, this is possible on 5 W cm Si. If the spacing is enlarged (while keeping the pore diameter roughly constant), pores with side branches and rough surfaces are formed. Again, the size of the bumps and branches corresponds to the size of the "hammer"- well formed pore around 2 µm diameter are to be expected.
 |
| Fig. 4 Macropores nucleated in n-type Si of 40 Wcm (4a) or 5 Wcm (b and c) under standard conditions. "Pitch" refers to the selected distance and pore diameter in µm. |
This already shows the interesting case: It is the third one – well-formed pores will now be found because every swing of the hammer produces the same result – cf. Fig. 4b).
The CBM thus not only gives a general recipe for the formation of well formed pores, it also specifies key ingredients and their interrelation. Obviously, changing the domain size gives a new degree of freedom in "designing" pores, it will be discussed later how this can be achieved. There is, however, another feature hidden in the correlation length which shall be discussed first: The correlation length can always be expressed on a time scale, too, leading to specific effects of the dynamics of the system. This can be best illustrated by considering the formation of pronounced side pores as it is expected if the pore dimension, determined e.g. by the size of the space charge region, is much larger than the correlation length or hammer size.
Generally, side pores tend to form if a) one or a few small hammers must produce a big pore, and b) the H-passivation of the side walls is so slow that a hammer can still attack the side walls above the pore tip (then most likely the {100} or {113} surfaces oriented into the direction of hole supply). The second condition demands that the pore has grown about one correlation length into the depth since the last branching in order to supply sufficient wall area. If these conditions are met, three predictions emerge: 1.) The diameter of the side pores is comparable to that of the main pore and given by LCo. 2.) Branches will be relatively regular and at a distance corresponding to the correlation length, and 3.) Branching can be suppressed if the current density is periodically reduced with a frequency somewhat larger than 1/tCo with tCo = time to grow the pore a distance LCo into the depth of the sample. This is to be expected because decreasing the current (which, at least under back side illumination conditions, is always focussed on the pore tip) forces the domain back to the pore tip and thus gives the side walls more time to passivate. While this picture is certainly oversimplified, it essentially supplies an approach towards the understanding of the remarkable influence of electrolyte type and current modulation on pore morphology as shown in Fig. 1.
Fig. 1c) shows rather well formed macropores in p-type Si as obtained in an organic DMF electrolyte; the response to current modulation is small. Using n-type Si with backside illumination, the standard method to produce well formed macropores, in a more naive view should result in even better pores because of the stabilizing effect of the back side illumination which tends to focus holes on the tip of the advancing pores. However, since the correlation length tends to be small in organic electrolytes (because of their reduced oxidizing power), and is reduced even more because of the lack of holes in n-type Si (which favors direct dissolution), we now have the case of one small hammer trying to produce a big hole – severe branching occurs on a scale directly showing the correlation length. as illustrated in Fig. 1b). Current modulations at various frequencies show no effect for small frequencies () but change the morphology dramatically at 33 mHz. Fig. 1a) finally shows that an aqueous electrolyte produces moderately well formed pores with little influence of the current modulation.
While much more could be said to the CBM at the general level, we will now discuss the properties of a single current burst and its relation to the correlation length as derived from theoretical considerations and interpretations of experiments. Besides the time allowed for H-passivation, which has been already discussed, the most important quantities are the relative strength of the direct dissolution and the oxidation, or Qd/Qox (which expresses itself in the valence of the total process) and tod. The following assignations can be made; speculative to some extent, but based on many observations (6 ,7 ,13 ,18 ,20 ,29 ):
The direct dissolution part always precedes the oxidation part of a CB and follows the nucleation of a CB – provided there are enough holes available. As reasoned before, there is a strong preference for <100> followed by <113> if <100> directions are unfavorable for hole capture. Avalanche effects, if occurring at all, will be expressed in this part of a CB. The valence of the process is variable (depending on the number of electrons injected into the conduction band (19), (26), but usually around 2. Direct dissolution is the preferred reaction for high electric field strength, lack of holes (always relative to what the electrolyte could process), and lack of reactive oxygen. The charge that can be transferred is limited by the oxide reaction taking over and/or the limitations concerning the necessary electron injection, i.e. by the chemistry of the system. Pores resulting from direct dissolution only may resemble fractal trees with <100> texture; an example is shown in Fig. 1 in (27).
Oxidation follows direct dissolution, it is initiated because the potential at the interface goes up (due to the collapse of the space charge region tied to interface states) and always has a valence of 4. It has a smoothing or electropolishing effect on pores (Oxidation by itself can not produce pores; cf. the section about oscillations). It is a self-stopping process because of the oxide formed and is the preferred reaction at high potentials, surplus of holes and sufficient availability of reactive oxygen. The sudden switch from well-formed macropores to tree-like fractal tress as reported in (27) can now be understood: Some of the initially formed macropores lose the race for holes supplied by backside illumination and fall back. At some critical point of the continuously decreasing hole supply, oxidation becomes too weak to sustain a sizeable correlation length and the dying pore continues for some time with mainly direct dissolution, producing a fractal <100> tree before it finally expires.
Changing Qd/Qox (for constant tod) thus provides the key for "designing" electrolytes. Following the guidelines above, it was possible,. e.g., to produce macropores in n+-type Si (5) (where only mesopores were observed before), to obtain microporous Si with organic electrolytes (28), or to produce extremely stable macropores in p-type Si (11).
It remains to mention a last, but very important feature of the CBM: Its stochastic nature provides for non-linear or critical phenomena – phase changes or separations, bifurcation or percolation points, etc. – which, as becomes increasingly clear, any model must include. The onset of stable oscillations, is a classical percolation limit in the CBM, other critical phenomena are the switch-over between pore types (suddenly as in the example in Fig. 1 in (27) or smoothly – depending on the nucleation history - as between macropores and micropores in p-type Si, the sudden change from <100> to <113> growth directions or the sudden disappearance of pores if some parameter (usually the current density) exceeds a limit. As has been shown in (18, 29), detailed investigations of the IV-characteristics by, e.g., impedance and transient spectroscopy yields more critical phenomena and demonstrate that the inflection points of the characteristics (and not the maxima) are of particular interest, signaling a switch-over in some basic mechanism. Some details about this can be found in these proceedings (13).
CONCLUSIONS
The stochastic approach to current flow through the Si electrolyte interface based on a few assumptions as expressed in the current burst model produces a large set of possible phenomena which overlaps very satisfactorily with the large set of observed phenomena. Possible phenomena not yet observed can be seen as predictions; so far many predictions came true, but many more have to be made. While much more work is needed to validate the model and to asset its range of applicability in Si, it appears that it may be applicable to some aspects of the electrochemistry of III-V semiconductors too (8).
ACKNOWLEDGMENTS
The authors are indebted to S. Langa who supplies results and new ideas from the III-V angle, K. Voigt who etched the macropores on p-Si in aqueous electrolyte, Dr. Popkirov whose experience and help in measurement techniques is invaluable, and Drs. Lehmann, Ozanam, and Wehrspohn for critical but constructive discussion.
REFERENCES
[2] J. Carstensen, R. Prange, H. Föll, J. Electrochem. Soc.,146, 1134 (1999)
[3] J. Carstensen, R. Prange, G. S. Popkirov, H. Föll, Appl. Phys. A., 67, 459 (1998)
[4] V. Parkhutik, S. Timashev, J. Appl. Phys., 87, 7558 (2000)
[5] M. Christophersen, J. Carstensen, H. Föll, in print, Phys. Stat. Sol. (a) 182, (2000)
[6] H. Föll, J. Carstensen, M. Christophersen, G. Hasse, in print, Phys. Stat. Sol. (a) 182, (2000)
[7] M. Christophersen, J. Carstensen, S. Rönnebeck, C. Jäger, W. Jäger, and H. Föll, submitted to J. Electrochem. Soc.
[8] S. Langa, I. M. Tiginyanu, J. Carstensen, M. Christophersen, H. Föll, J. Electro-chem. Soc. Lett., 3 (11), 514 (2000)
[9] M. Christophersen, P. Merz, J. Quenzer, J. Carstensen, and H. Föll, to be pub-lished in Sensors and Actuators A (2000)
[10] J. Carstensen, M. Christophersen, H. Föll, Mat. Sci. Eng. B, 69-70, 23 (2000)
[11] M. Christophersen, J. Carstensen, A. Feuerhake, H. Föll, Mat. Sci. Eng., B 69-70, 194 (2000)
[12] F. Ozanam, J.-N. Chazeviel, A. Radi, M. Etman, Ber. Bunsenges. Phys. Chem., 95 (1991)
[13] G. Hasse, J. Carstensen, H. Föll, proceedings of the ECS meeting, Arizona, (2000)
[14] E. Yablonovitch, D.L. Allara, C.C. Chang, T. Gmitter, and T.B. Bright, Phys. Rev. Lett., 57, 249 (1986)
[15] T. Baum, D. J. Schiffrin, J. of Electroanal. Chem., 436, 239 (1997)
[16] S. Rönnebeck, J. Carstensen, S. Ottow, H. Föll, Electrochemical and Solid-State Letters, 2, 126 (1999)
[17] V. Lehmann, J. Electrochem. Soc., 140, 2836 (1993)
[18] J. Carstensen, M. Christophersen, G. Hasse, H. Föll to be published Phys. Stat. Sol. (a) 182, (2000)
[19] V. Lehmann, H. Föll, J. Electrochem. Soc., 137, 653 (1990)
[20] M. Hejjo Al Rifai, M. Christophersen, S. Ottow, J. Carstensen, H. Föll, J. Electro-chem. Soc., 147 (2), 627 (2000)
[21] M. J. J. Theunissen, J. Electrochem. Soc., 119, 351 (1972)
[22] V. Lehmann, S. Stengl, A. Luigart, Mat. Sci. Eng. B, 69-70, 11 (2000)
[23] A. Valance, Phys. Rev. B, 52, 8323 (1995)
[24] Y. Kang, J. Jorne, J. Electrochem. Soc., 140, 2258 (1993)
[25] V. Lehmann, U. Gösele, Adv. Mat., 4, 114 (1992)
[26] E. K. Propst, P.A. Kohl, J. Electrochem. Soc., 141, 1006 (1994)
[27] C. Jäger, B. Finkenberger, W. Jäger, M. Christophersen, J. Carstensen, H. Föll, Mat. Sci. Eng., B 69-70, 199 (2000) to be published
[28] to be published
[29] G. Hasse, J. Carstensen, G. S. Popkirov, H. Föll, Mat. Sci. Eng., B 69 - 70, 188 (2000)