PDF-Version of this document (0.5 MB)

Percolation model for the current oscillation in the Si-HF system

J. Carstensen, R. Prange, and H. Föll

Faculty of Engineering

Kaiserstr. 2

24143 Kiel

Germany

Abstract

Applying sufficiently large anodic potentials, the dissolution of silicon in fluoride electrolytes causes current oscillations which are correlated with an anodic growth of silicon oxide. We present the first complete model of these current oscillations based on electric field defined dynamics of local oxide growth and dissolution and an appropriate synchronization mechanism. The physical character of the local oscillators depends on non-linear oxide growth characteristics in high electrical fields. A next neighbor coupling between independent local oscillators based on the geometry of oxide growth leads to percolation areas of about 100 nm as a result of Monte Carlo simulations. This percolation provides an intrinsic synchronization of the local oscillators leading to macroscopic oscillations. The calculated parameters, e.g. frequency, current over time, oxide layer thickness, capacitance and the roughness of the surface, are in good agreement with experimental results.

PACS: 64.60.Ak, 68.45.-v, 82.40.-g, 82.45.+z, 82.65.-i

Introduction

The silicon hydrofluoric acid contact shows several not yet well understood phenomena, including the quite complicated IV-characteristics (Fig. 1), the formation mechanisms for pores with diameters from the nm to the µm range, and the current or potential oscillations which occur when applying high anodic bias U_an [1,2,3,4]. In situ analysis with e.g. ellipsiometry [5,6,7], IR-spectroscopy [8,9] or atomic force microscopy [10] demonstrate a strong coupling between the current oscillation and the growth of the oxide layer and provide information on the thickness and morphology of the oxide layer as a function of the oscillation phase. However, no consistent model of current oscillation at the Si-electrode exists so far.

In describing the current oscillation one has to face the problem that the current oscillations which are coupled to the growth of an oxide layer less than 10 nm thick are synchronized on areas of up to several cm². Therefore in modeling the oscillations, two essential ingredients are needed: a) a mechanism for localized oscillations on an area of the electrode that must be on the order of magnitude of the oxide thickness, and b) a mechanism to synchronize these local oscillators on much larger areas. In a first step we discuss a model of the localized oscillators, i.e. the mechanism of periodic growth and dissolution of small (nm scale) oxide areas. In a second step we suggest an intrinsic synchronization mechanism which does not need an external triggering as has been postulated in [11]. In a third step we introduce a desynchronization mechanism, and finally combine all ingredients to a fully quantitative model that yields analytical results and, via Monte Carlo simulations, a wealth of data concerning details of the oscillations.

The Model

For slow oscillations we propose in accordance with experimental results [12] that the complete current density J_ox generates silicon oxide, increasing the thickness s of the oxide layer. Taking into account the chemical dissolution of the oxide, we get

(1)

b is a geometrically determined parameter and a purely chemical dissolution rate.

As already stressed by several authors [13, 14] the ion transport through the oxide layer is the key for the understanding of the oscillation phenomenon. We propose the electric field across the oxide to be a nonlinear driving force for the ion transport through the oxide, causing a "ionic breakthrough" when the electric field in the oxide approaches a maximum value E_max leading to a oxide-thickness independent constant current J_ox. While the oxide thickness increases, the electric field decreases without reducing the ion transport through the oxide. At a minimum value E_min the oxide growth stops. In analogy to an electronic breakthrough, we assume that after starting the ion transport through the oxide, the electric field can be reduced drastically without reducing the ion current. Leaving aside a microscopic picture for the ion transport and only pointing out that the ions have to pass a 2 to 8 nm thick oxide layer, a mechanism emerges, centering around a narrow channel or pore through the oxide, which is opened at high field strength. Defining the anodic potential U_an, and , the local oxide layer thickness increases by

Ds=s_max - s_min, (2)

before the channel is "closed" again. This simple local model would allow for a homogeneous growth (and oscillations) of the oxide layer thickness and could be evaluated analytically. However, it will not account for macroscopic oscillations that can only be observed, when a large number of local oscillators are synchronized. Since E_min and E_max are just lower and upper limits for the ionic breakthrough and the closing of the channels, we have to account for the statistical nature of these events and define two functions W(E) and R(E) to define the probability for the "begin" and the "end" of a ionic breakthrough within a time Dt on an area DA. The statistical nature of the proposed process as well as nonhomogeneous oxide layer thickness at any one time during an oscillation, would necessarily cause a desynchronization of the local oscillators, and no macroscopic oscillations would be observed if the local currents are summed up with random phases.

A synchronization mechanism for neighboring local oscillators is schematically illustrated in Fig. 2. Once a channel opens, it is plausible to assume an isotropic growth of silicon oxide from the tip of the channel, leading to a roughly semi-spherical oxide-"inclusion". Since the volume of the oxide changes by a factor of two, a semi-sphere of about the same size as in the bulk silicon must occur at the electrolyte-oxide surface, leading to an increased effective oxide surface. As a consequence, we suppose a lateral growth of the oxide of the same order of magnitude as the growing oxide thickness Ds/2. Thus a neighboring channel, which supposedly starts at a later point in time, must produce less oxide before it stops again; its stop-point is thus already much closer to the stop-point of the first channel; we could say that its dynamics are enhanced until it catches up with the first oscillator. After a few cycles, the two local oscillators will be perfectly synchronized. This synchronized growth of neighboring oxide regions via a "next neighbor coupling" can be implemented in a Monte Carlo algorithm and leads always to synchronized macroscopic oscillation.

A desynchronization mechanism, however, also exists, it is illustrated in Fig. 2. Once a channel opens, the current density is locally increased, leading to increased ohmic and diffusion losses which locally reduces the potential across the oxide layer (see Fig. 2). This reduces the electric field strength in the neighborhood of an active channel, and therefore the probability for a "breakthrough" next to an active pore.

Applied to the example given before, this effect would slow down the dynamics of the oscillator until it is perfectly out of phase. In consequence not all areas of the oxide layer can grow at the same time, which means a desynchronization of the macroscopic oscillation. Assuming a reduction of the current density at a distance r from the channel, the ohmic losses are calculated by

. (3)

As a first approximation this function is used to describe the potential and diffusion losses of the anodic potential in the Monte Carlo simulations, with A as a fitting parameter.

Results and Discussion

Our model contains

• Local oscillators caused by oxide growth in an ionic break-through mechanism,

• synchronization of local oscillators by next neighbor interaction due to lateral growth at the break-through channel tips and percolation,

• desynchronization by ohmic or diffusion losses of the anodic potential at local oscillators.

The performance of the model and its dependence on parameter is analyzed by Monte Carlo simulations. Before discussing the general results, some analytical formulae for the case of well synchronized oscillations will be presented. For very slow oscillations the time for building up oxide can be neglected compared to the time for dissolving oxide. The time T for one oscillation period is therefore . Using the electric field defined dynamics for the local oscillators as discussed above, we find

. (4)

For extremely diluted HF-electrolytes, leading to a slow dissolution rate , the oscillation time then increases linearly as a function of the applied voltage, as experimentally shown in [15]. For stable oscillations the mean oxide layer thickness does not change, i.e. applying Eq. 1 we find

. (5)

The bar denotes the averaging across the complete electrode area and over one oscillation period. The mean oxidizing current thus is

. (6)

Inserting Eq. (6) in Eq. (4) we find

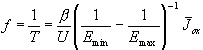. (7)

This linear correlation between oscillation frequency f and mean current density has experimentally been shown in [15]. So our model allows to quantify several experimental results by Eq. (4), (6) and (7), for which until now no interpretation was supplied.

Stable current oscillation as a result of the Monte Carlo simulation are demonstrated in Fig. 3A. It should be mentioned that a random distribution of oxide thickness was chosen as the starting point, nevertheless stable oscillations occur after just on period. Figs. 4a-4d show the corresponding maps of the oxide layer thickness on an 200nm x 200nm area for subsequent phases of one oscillation period. Most important is the lateral coupling of more than 100 nm great areas, although there is no mechanism implemented in the model to force such large areas to nearly the same thickness. The lateral synchronization of these areas is caused by percolation due to the local coupling mechanism, which in consequence leads to synchronization in the time domain and to macroscopic oscillation. If the anodic potential is reduced or the parameter A in Eq. (3) (and thus desynchronization) is increased, no macroscopic current oscillations occur. The corresponding oxide thickness map (s(x,y)) of Fig 5 shows a "random" distribution for s(x,y) and the histogram in Fig. 5 may be interpreted as the average of the histograms in the oscillating case of Fig. 4.

Using Fig. 2 we can define a minimum distance d of two channels which can exist a the same moment. The critical field strength E_min has to be reached at d, which depends on the actual thickness, the applied potential, the probability function W(E) and the ohmic losses DU(r). If d is large, no third channel can open, before one of the two existing channels is closed, the oxide can not grow homogeneously and is rather rough. In contrast, if d is small, the oxide layer can grow nearly homogeneously, because the semi-spherical oxide-"inclusions" overlap.

It is now useful to define a geometric parameter x(d,U) which determines the ratio between the strength of the synchronization and the desynchronization mechanisms. Beyond a critical value

(8)

macroscopic oscillations will be observed.

Monte Carlo simulations were performed for the case of extremely diluted hydrofluoric acid with a dissolution rate of . The values of the critical electric field strength E_min=5*10⁶ V/cm and E_max=3*10⁷ V/cm have been taken from experimental results in [12]. We assume a constant oxidizing current of 0,07 fA through each open channel. For the desynchronization described by Eq. 3 we take A=0.2 V nm. For an anodic potential of 2 V we find stable oscillations as plotted in Fig. 3A. The corresponding oxide layer thickness’ maps of four subsequent phases of one oscillation period are plotted in Fig 4a-d (The times are marked in Fig. 3A). At point a) we find a nearly homogeneous thick oxide layer, which is dissolved with a constant rate . Consequently we find in Fig 3B a straight line for the reduction of the mean oxide layer thickness. At point b) most of the oxide is still thinning, while first oxide areas show ionic conductivity and are growing quickly. Point c) demonstrates the phase of the oscillation with maximum oxide current. On about half of the area the oxide is only dissolving, while on the other half the oxide has already reached its maximum thickness. In point d) the cycle is almost closed. Most areas show thick oxide layer and are only chemically dissolved, while some remaining areas with thin oxide allow for ionic breakthrough to increase their thickness.

The calculated data of the Monte Carlo simulation can be compared with experimental results, which are related to the oxide layer thickness, e.g. the oxide layer distribution function D(s), which tells us, how many areas of the oxide show a thickness s. Comparing our calculated histograms in Fig. 4a-d with the measured result for D(s) in [12], we find an almost perfect agreement for all phases of the oscillation.

With the distribution function D(s) from the histograms we can, e.g., calculate

the mean oxide thickness , (9)

the capacitance , (10)

and the oxide roughness , (11)

which are plotted in Fig. 3B-D.

It is a particularly important feature of the model that the roughness of the oxide surface is not only constantly refreshed, but changes periodically which tentatively agrees with measurements [10]. The roughness of the oxide layer may cause problems for the interpretation of experimental results, e.g. when comparing the variations of the oxide layer thickness with the variations of the capacitance in the oscillating regime. The capacitance then must not follow the thickness variation as in the case of a smooth oxide and is not necessary to invoke a periodically varying dielectric constant as, e.g., in [7] to explain the data.

If for the calculation of the capacitance not , but correctly, is used, measured and calculated data for constant epsilon are in perfect agreement [12].

References

1. D.R. Turner: J. Electrochem. Soc., 105, 402 (1958)

2. R.L. Smith, S.D. Collins: J. Appl. Phys., 71, R1 (1992)

3. H. Föll: Appl. Phys. A, 53, 8 (1991)

4. V. Lehmann: J. Electrochem. Soc., 143, 1313 (1996)

5. J. Stumper, R. Greef, L.M. Peter: J. Electroanal Chem., 310, 445 (1991)

6. D.J. Blackwood, A. Borazio, R. Greef, L.M. Peter, J. Stumper: Electrochimica Acta, 37, 889 (1992)

7. M. Aggour, M. Giersig, H.J. Lewerenz: J. Electroanal. Chem., 383, 67 (1995)

8. J. Rappich, H. Jungblut, M. Aggour, H.J. Lewerenz: J. Electrochem. Soc, 141, L99, (1994

9. F. Ozanam, C. da Fonseca, A. Venkateswara Rao, J.-N. Chazalviel: Applied Spectroscopy, 51, 519 (1997)

10. O. Nast, S. Rauscher, H. Jungblut, H.J. Lewerenz: J. Electroanal. Chem., in press

11. J.-N. Chazalviel, F. Ozanam: J. Electrochem. Soc., 139, 2501 (1992)

12. R.Prange, J. Carstensen, H. Föll: ECS meeting San Diego 1998, this proceedings

13. H. Gerischer, M. Lübke: Ber. Bunsenges. Phys. Chem., 92, 573 (1988)

14. J.-N. Chazalviel: Electrochimica Acta, 37, 865 (1992)

15. F. Ozanam, J.-N. Chazalviel, A. Radi, M. Etman: Ber. Bunsenges. Phys. Chem., 95, 98 (1991)

Fig. 1: The IV- characteristics of the silicon-hydrofluoric acid contact shows the different phenomena from generation of porous silicon, electropolishing and electrochemical oscillations at higher anodic bias.

Fig. 2: Schematic view of a "ionic breakthrough". Due to the oxidizing current a roughly semi-spherical oxide inclusion is growing from the tip of channel 1. Ohmic or diffusion losses reduce the potential drop across the oxide layer around the channel. This reduces the probability for the breakthrough of a second channel. The distance between two channels defines the possibility of percolation and therefore macroscopic oscillation.

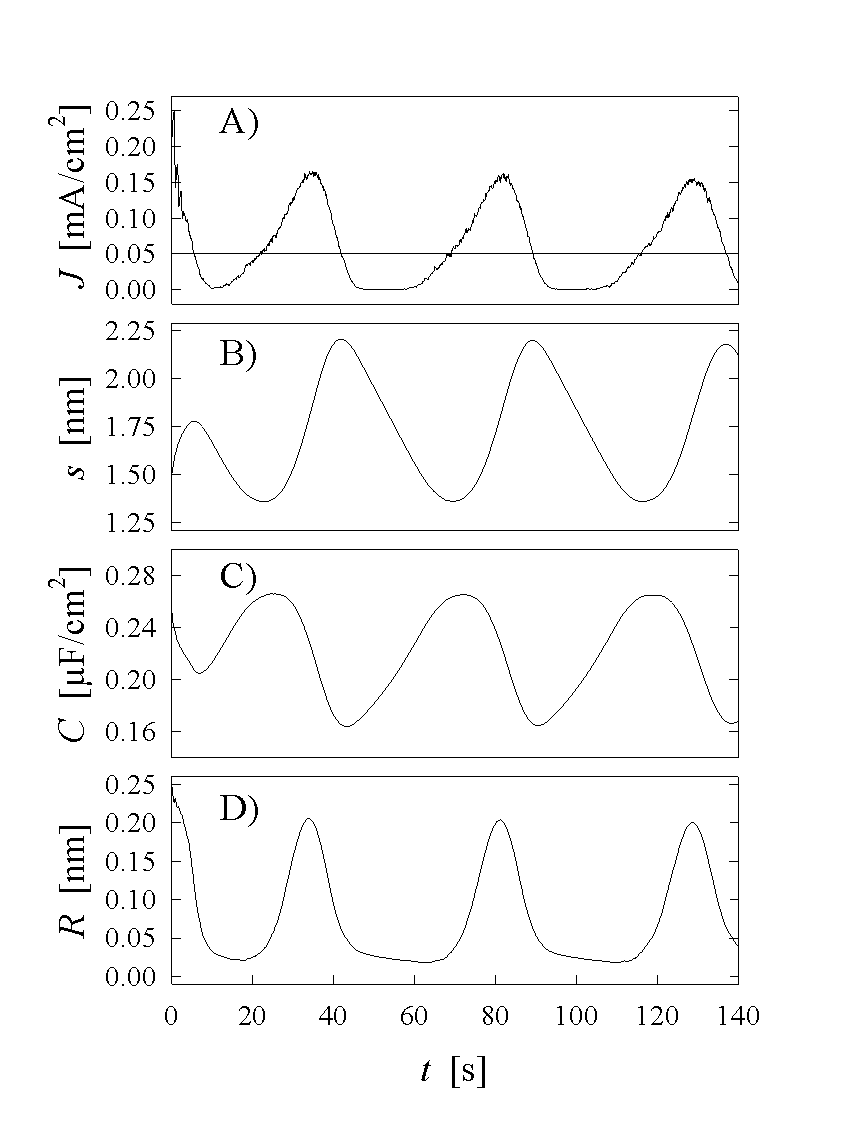
Fig. 3: The oscillation current A), the mean oxide thickness B), the capacitance of the oxide layer C) and the roughness of the oxide layer D) are plotted as results of the Monte Carlo simulation. This slow and stable oscillations consist of two phases. From point a) to point b) is the phase of purely chemical dissolution of the oxide layer. From b)-d) on each oxide area a "ionic breakthrough" builds up the oxide layer again.