PDF-Version of this document (1 MB)

Transient Current Measurements on the Si-HF System as a Direct Image of the Oxide Thickness in the Oscillation Regime

R. Prange, J. Carstensen, H. Föll

Faculty of Engineering, Kaiserstraße 2, D-24143 Kiel, Germany

Abstract

Applying sufficiently large anodic potentials, the dissolution of silicon in fluoride electrolytes causes current oscillations which are correlated with an anodic growth of silicon oxide. The dynamics of oxide growth and dissolution is studied by transient current measurements at various phases of the oscillation. An interpretation of the transient currents as a direct representation of the oxide thickness distribution allows the calculation of the oxide capacity, showing excellent quantitative agreement with in situ FFT impedance measurements. The analysis of an averaged continuity equation yields absolute values for dissolution rate and oxide thickness.

PACS: 64.60.Ak, 68.45.-v, 82.40.-g, 82.45.+z, 82.65.-i

Introduction

Silicon electrodes in fluoride containing electrolytes exhibit a number of interesting phenomena, including micro-, meso-, and macro- porous silicon formation, electropolishing and current-voltage oscillations [1, 2, 3].

Independent of the doping, current- as well as voltage-oscillations are observed. While results of voltage oscillations are published rarely [4], a number of papers deals with the investigation of current oscillations, which are supposed to be strongly coupled to the growth of the silicon oxide on the surface of the electrode. In situ analysis with ellipsiometry [5, 6, 7], IR-spectroscopy [8, 9], microwave reflectivity [10], atomic force microscopy [11] have been performed in order to obtain detailed information on the thickness and the morphology of the oxide layer as a function of the oscillation phase and thus to examine the dynamics of the oxide growth and dissolution.

Gerischer [12] emphasized that the migration of ions through the oxide is the key for understanding the oscillations. A model of local oscillators externally synchronized in order to get macroscopic oscillations has been discussed by Chazalviel et. al. [13, 14], but up to now, no microscopic model has been presented.

Measurements of the current transients obtained after changing the anodic potential to open circuit potential are a very useful tool in this field; the technique has been used, e.g., to analyze the oxide thickness and its homogeneity at different phases of the oscillation [15]. In this paper we present measurements together with a new model that allows fully quantitative interpretations of the current transients. Within the framework of the model it is possible to quantitatively extract parameters, as e.g. dissolution rate, oxide thickness, distribution function of the oxide thickness, or the capacitance of the oxide, in full agreement with independent measurements.

Based on this analysis, a microscopic picture of the local oscillators and their synchronization emerges, which will be presented in a separate paper [22].

Experimental setup

The experiments were performed with {100} oriented p-Si wafers of 1 Wcm resistivity. Ohmic contacts were provided by p+-doping of the back side and GaIn alloy. The samples were etched in diluted HF solution to remove the native oxide layer.

The electrochemical cell was made of PVC with an active electrode area of 0.3 cm2. The counter electrode was a Pt grid. The reference electrode was a saturated calomel electrode (SCE) connected to the cell by means of an Agar-Agar bridge with a Luggin capillary mounted close to the working electrode surface.

The electrolyte was a solution of 0.1 w% HF and 1 M NH4Cl (volume ratio: 1:1), pH 2.8, and was circulated through the cell by a peristaltic pump.

The current-time and in situ FFT-impedance spectroscopy (FFT-IS) measurements were carried out using a home made potentiostat and FFT-impedance spectrometer as described in more detail in [16, 17].

Experimental Results and Specific Data Representation

Applying a potential of 4.5 Volt vs. SCE leads to slow current oscillations as shown in Fig. 1a. These oscillations with a frequency f < 0.02 Hz are well reproducible and allow the investigation of the current transients as described e.g. in [12, 15, 18, 19]. At several stages of the oscillation the potential is stepped to open circuit potential, i.e. the potential , for which the current i is zero in a steady state. Subsequently the current is measured as a function of time. The resulting current-time curves are shown in Fig. 1b; their relation to the current oscillation curve is indicated by arrows.

The raw measurements are not suitable for direct analysis; a data compression based on appropriate statistics is necessary. For reasons that will be elucidated in the discussion, we choose a special procedure: First we determine numerically the average current density between two succeeding measurements. Next we determine numerically the mean for all current transient profiles, which is defined as

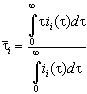, (1)

take the difference between the mean times of succeeding transient currents, and finally divide by , the time difference between the two measurements. The resulting quotient is termed "relative oxide growth" for reasons clarified in the discussion. If we now plot the relative oxide growth vs. average current density (making, however, one small correction in evaluating as will be discussed later), we obtain the data shown in Fig. 2.

Obviously, the data-compression procedure succeeded in reducing highly nonlinear phenomena into two straight lines with identical slope but different offset. The oscillation in question moves along the dashed line. In the case of an undamped oscillation (which we do not have in this particular case), the dashed line would close; our representation therefore can be considered as a suitable phase-space for the current oscillations at Si-electrodes.

In what follows, we will show that Fig. 2 - which, as we like to emphasize, represents exclusively measured data - can be reproduced theoretically from first principles if one uses a simple model of the oxide growth dynamics at a oscillating interface. Our model and its implications for current transients is partially at variance with previously suggested models [22], but allows for the first time to make quantitative predictions about a number of phenomena relating to the Si-electrode, which can be verified in independent experiments - one example will be given in the remainder of the paper.

Model and Discussion

It is generally accepted that under open circuit condition the surface oxide is chemically dissolved, reducing the local thickness of the oxide layer s(x,y,t) with the velocity ds/dt=-a, which is assumed to be constant. After some time, only the so-called thin "sub-oxide layer" remains, whose dissolution generates the observed transient current due to its substoichiometric composition at the interface with the bulk silicon [12, 15, 19].

Defining our modell by the following fundamental assumptions, a quantitative interpretation of the transient current curves is possible:

1) all of the transient current is generated by dissolving suboxide.

2) the released charge per unit area g for the suboxide layer is constant and independent of the phase of the oscillation.

3) the time for dissolving the suboxide is small in comparison with the time for dissolving the oxide. This means that the thickness of the sub-oxide layer is small compared to the average thickness of the oxide present during the oscillations.

With these presumptions each unit area with oxide thickness s adds a charge g at the time t=(s / a) to the transient current i(t). Thus i(t) dt =g D(s =at) ds with D(s) being the sum of all areas with oxide thickness s at t =0. In other words, D(s) is the thickness distribution of the oxide at any given point of the oscillation. In consequence, the transient current curves in Fig. 1b show the exact distribution of the oxide thickness at the phase of the oscillation where the transient current measurement was started. Fig. 1b therefore contains a thickness scale (top) in addition to the time scale (bottom). In the current minimum of the oscillation (Fig. 1b; measurements 6-9), the peak width and therefore the distribution of oxide thickness D(s) is narrow, indicating that the lateral distribution of oxide thickness is quite homogeneous. In this phase the mean thickness is decreasing while the shape of the transient peak does not change significantly. This indicates a laterally homogeneous Ds of the oxide. The dissolution velocity a of a "static oxide" (an expression used for the oxide during the transient current measurements) thus can be obtained by calculating D s/D t, or D s=a D t .

In contrast, the measurements 1-3 show two peaks; a decreasing one for areas with thin oxide and a growing peak for areas with thick oxide. This obviously describes the phase of oxide growth, which correlates well with the maximum in the oscillation current. It suggests that one part of the oxide surface is still chemically dissolved while in other areas the oxide thickness is growing, demanding an inhomogeneous lateral distribution of oxide thickness. The lateral dimension of the areas with thin and thick oxide will be discussed later.

Recognizing that the current peak during oscillation coincides with the growth of the oxide, we assume for a first quantitative analysis that all of the current builds up oxide. In the phase, when least oscillation current is measured (Fig. 1b; e.g. measurement 8-9), the dominant reaction then must be chemical etching of the "oscillating oxide" (an expression used for the oxide during the oscillations). The time interval between measurement 8 and 9 is Dt = 12 sec according to Fig. 1a. During this time interval only dissolution of the "oscillating oxide" takes place, its thickness decrease, as given above, is Ds=a D t=a 20 sec according to Fig. 1b. However, Ds must also been given by Dt, with being the chemical dissolution rate of an "oscillating oxide". Putting both relations together, we obtain for the (obviously enhanced) dissolution rate of an "oscillating oxide" in the non-growth regime

=(Dt / Dt) a=1.7 a. (2)

It is easily verified that all data points in the "non-growth regime" of the oscillating oxide (roughly points 6 - 9) would yield the same value.

We are thus forced to consider two different dissolution velocities: a corresponds to the chemical dissolution of a "static oxide" when open circuit potential is applied and no current flows, is the dissolution rate of an "oscillating oxide".

There may be several reasons for this increased dissolution rate, e.g. a potential dependence of the oxide dissolution rate or a roughening of the oxide surface, leading to an increased effective surface of the "oscillating oxide". As will be shown later, the factor 1.7 is nearly independent of the oxide thickness and therefore also nearly independent of the potential across the Helmholtz layer or the field strength within the oxide layer, which will change will change significantly with the oxide thickness. This leads us to believe, that the predominant mechanism for the enhanced dissolution is a roughening of the oxide surface during the oscillations.

Inherent in the above assumptions is a local continuity equation, which will be formulated and checked. For each point of the "oscillating oxide" layer the net growth rate per unit area is

. (3)

Jox is the current density, is a purely geometrically determined parameter for building up silicon oxide, assuming a density of 2.1 g/cm3, and is the effective dissolution rate of the "oscillating oxide".

Eq. (3) can not be tested experimentally, because it is impossible to measure the parameters ds/dt, Jox and as a function of location and time directly. But since we can extract the average current density from the oscillation current, and the change of the "oscillating oxide" thickness between time ti and ti+1 from the transient currents, we can use Eq. (3) in an integral form.

For a quantitative description of an inhomogeneous oxide layer, which is build up by a current varying in time and location and dissolved by a generally inhomogeneous dissolution rate, we must integrate Eq. (3) in space and in time. The integration over the inhomogeneous oxide layer yields for the average oxide growth rate

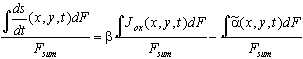, (4)

with .

For the quantitative analysis of the transient current, we need the change of the average "oscillating oxide" thickness between two measurements at time ti and ti+1. Using Eq. (3) we find

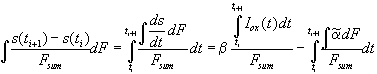. (5)

We define a mean dissolution rate

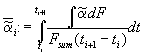. (6)

Taking into account the interpretation of the transient current to be the distribution function of the oxide thickness s =a t, we calculate the mean oxide thickness

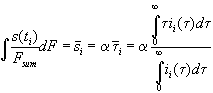, (7)

ii(t) is the transient current of measurement No. i.

The second assumption of our model (the total oscillation current generates oxide) allows to calculate the mean current used for building up oxide between two measurements of the transient current

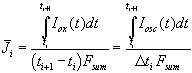. (8)

Including Eq. (6)-(8) into Eq. (5) we get

. (9)

Despite of the fact, that Eq. (9) contains a number of integrals, it displays the same physical meaning as Eq. (3). A change of oxide layer thickness, described by , is caused by an oxide building current density J and an oxide dissolving rate . But in contrast to Eq. (3) and are measurable parameters. If is constant and our assumptions are correct, a linear relation between the parameters and is predicted.

Before applying Eq. (9) to our measurements, we will evaluate the integral , which yields the total charge of the suboxide layer and which so far was assumed to be constant. Fig. 3 shows that this charge is not constant within the oscillation period. While the oscillation current is small, the charge has its maximum value and is approximately constant. This result violates our fundamental assumption 2), if taken on face value. There are at least three possible answers for the reduction of the overall suboxide charge: a) the charge per unit area in the suboxide layer is not constant and depends on the phase of the oscillation; b) there are regions without oxide and therefore without suboxide in certain periods of the oscillation; c) for parts of the oxide layer suboxide charge is present, but does not contribute to the current. Some strong arguments for the third interpretation will be discussed later.

The consequent implementation of assumption c) thus means to replace in Eq. (1) by its maximum value, which is the best value for the charge of the completely oxide covered area. We change Eq. (6) to

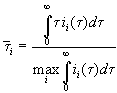. (1a)

With Eq. (9) and Eq. (1a) in mind, which quantify the recipe given for obtaining Fig. 2, we can take a fresh look at Fig. 2. We realize now that the diagram shows vs. as given in Eq.(9). Obviously most points lie on two almost parallel straight lines, which have been calculated by a linear regression. Within one period of the oscillations the dynamic parameters change from one set, represented by line B, to a second parameter set, represented by line A, and return to line B.

We first discuss line A. All points on these line correspond to the maximum charge in Fig. 3. For we find according to Eq. (9) , which coincides well with the result of Eq. (2). We emphasize that the two methods, the investigation of the movement of the peak maximum using Eq. (2) and the calculation of the overall dissolution of the oxide with Eq. (9), are independent and show the same enhanced dissolution of the "oscillating oxide". It should be mentioned that using in Eq. (1a) was an essential choice, otherwise we would not obtain the same factor for both methods. Despite of the fact that the oxide thickness changes by a factor of two for the data points on line A, the enhanced chemical dissolution of the "oscillating oxide" is remarkably constant. As already mentioned above, this is a strong indication for an enhanced dissolution mechanism of the oxide that is independent of applied potentials.

The absolute value of a can be calculated from the slope of the straight line A, which is . Taking the parameter b=0.74 nm/sec cm2/mA we find a=0.04 nm/sec. This is in good accordance with e.g. Sere et al. [20], who measures nm/sec as the dissolution rate of an anodic oxide grown in water.

Now we can calculate the absolute thickness by using Eq. (7) and the lateral distribution function D(s) of the oxide layer and thus obtain the thickness axis in Fig. 1b. The thickness varies approximately from a minimum value of 3 nm to a maximum value of 7 nm. The lateral inhomogeneity (=roughness) is described by the differences of the oxide thickness at each moment. This value varies from roughly 4 nm at the maximum of oscillation current down to 2 nm in the minimum.

The fitted line B exhibits approximately the same slope as line A leading to the same value for a. It shows a strong offset, which may have several reasons: i) there is a current density component in Josc, which does not build up oxide; ii) the dissolution of oxide is strongly enhanced in the corresponding period of the oscillation; iii) there exist areas of the oxide, for which no suboxide charge is measured in the transient current peak. As discussed before, a nonoxidizing current and an electrochemically enhanced dissolution of oxide should depend on the Helmholtz layer potential and therefore on the oxide layer thickness. Since oxide layer thickness varies by a factor of two for the measurements on line B resulting only in an offset between both lines, a potential dependent dissolution rate is rather unlikely. In addition, an enhanced dissolution rate by a factor 3.5 inherent in the offset, would be difficult to explain.

Thus we are lead to believe that certain regions of a growing oxide do not show a suboxide charge. This assumption is in accordance with the results in Fig. 2 which show that some suboxide charge is missing when the oscillation current peaks. Including this interpretation into Eq. (9), a simple answer for the offset between both straight lines can be given.

For the mathematical description of the complete oxide area we introduce a distribution function L(s) in analogy to D(s) describing the areas with oxide thickness s, which do not add suboxide charge to the transient current. The correct mean oxide thickness is now calculated by

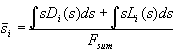. (10)

Defining 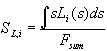Eq. (9) is modified:

. (11)

The measurement shows an additional offset between the lines A and B of 1.7 in Fig. 2, yielding

. (12)

Eq. (12) implies a constant growing rate of the L-regions with a velocity h=1.7 a. The coincidence between the value of h and may be accidentally, but just as well it could be a hint on the dynamics of oxide growth. An explanation of the missing suboxide charge must be find for a model of the oscillations [22].

Interpreting the transient current as an almost direct measurement of D(s) we should be able to predict physical parameters of the oxide layer which depend on its thickness. The most prominent candidate for this check is the oxide layer capacitance. The very slow oscillations observed for low HF concentration allow for in situ FFT-IS measurements. Fig. 4 displays measurements of the oscillation current density and the corresponding capacitance Cox for the same sample as above. The Capacitance was calculated from the FFT-IS data by fitting an equivalent circuit consisting of a parallel RC-circuit Cox and Rox followed by a serial resistance Rser. The capacitance per unit area for the inhomogeneous oxide layer using our model is calculated by

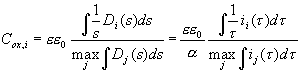, (13)

i.e. as a parallel connection of all oxide layer capacitances. In evaluating this equation, we first try to understand the phase shift between the oscillation current density and the capacitance. We have found the oscillation to be a periodical change from a phase of growing oxide to a phase of decreasing oxide thickness. Since the capacitance increases when oxide thickness decreases and vice versa, we may expect the maximum and minimum of the capacitance, when the integral oxide thickness does not change, i.e. . With Eq. (4) and using the constant value of , we find the corresponding current value 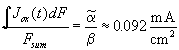. This value is plotted in Fig. 4a. Whenever the oscillation current density equals this value, a period of growing oxide changes to a period of decreasing oxide thickness or vice versa. As predicted, at this times the capacitance shows its extremas, being at minimum before the oxide thickness decreases and a maximum before the oxide thickness increases. This is a third independent check for the correct evaluation of the dissolution rate of the "oscillating oxide".

Taking e=3.9, which is the value for a thermal oxide, a=0.04nm/s as calculated before, and integrating the measured transient currents in Eq. (13), we obtain a theoretical capacity per unit area, which is plotted as a second curve in Fig. 4b. The bold vertical lines limit the range, corresponding to those points in Fig. 2, for which the full suboxide charge is measured. Only in this range the correct inverse oxide thickness is obtained when integrating . Comparing the FFT-IS results and the calculated capacitance, we find an excellent agreement in all parameters. The offset of about 10% for the absolute values of the capacitance is remarkably small, especially in view of the number of independent measurements needed to generate these data. The offset may easily be explained by a slightly increased dielectric constant e for the anodic oxide compared to e of a perfect thermal oxide, which is rather to be expected.

Acknowledgement

The authors are grateful to Dr. G. Popkirov for his contributions.

References

1. D.R. Turner: J. Electrochem. Soc., 105, 402 (1958)

2. R.L. Smith, S.D. Collins: J. Appl. Phys., 71, R1 (1992)

3. H. Föll: Appl. Phys. A, 53, 8 (1991)

4. V. Lehmann: J. Electrochem. Soc., 143, 1313 (1996)

5. J. Stumper, R. Greef, L.M. Peter: J. Electroanal Chem., 310, 445 (1991)

6. D.J. Blackwood et al.: Electrochimica Acta, 37, 889 (1992)

7. M. Aggour, M. Giersig, H.J. Lewerenz: J. Electroanal. Chem., 383, 67 (1995)

8. J. Rappich et al.: J. Electrochem. Soc, 141, L99 (1994)

9. F. Ozanam et al.: Applied Spectroscopy, 51, 519 (1997)

10. H.J. Lewerenz, G. Schlichthörl: J. Electroanal. Chem., 327, 85 (1992)

11. O. Nast, S. Rauscher, H. Jungblut, H.J. Lewerenz: J. Electroanal. Chem., in press

12. H. Gerischer, M. Lübke: Ber. Bunsenges. Phys. Chem., 92, 573 (1988)

13. J.-N. Chazalviel, F. Ozanam : J. Electrochem. Soc., 139, 2501 (1992)

14. F. Ozanam, N. Blanchard, J.-N. Chazalviel: Electrochimica Acta, 38, 1627 (1993)

15. F. Ozanam et al.: Ber. Bunsenges. Phys. Chem., 95, 98 (1991)

16. G.S. Popkirov, R.N. Schindler: Rev. Sci. Instrum., 63, 5366 (1992)

17. G.S. Popkirov, R.N. Schindler: Electrochimica Acta, 39, 2025 (1994)

18. A.E. Gershinskii, L.V. Mironova, E.I. Cherepov: phys. stat. sol. (a) 38, 369 (1976)

19. M. Matsumura, S.R. Morrison: J. Electroanal. Chem, 147, 157 (1983)

20. C. Serre, S. Barret, R. Hérino: J. Electrochem. Soc., 141, 2049 (1994)

21. J.-N. Chazalviel: Electrochimica Acta, 37, 865 (1992)

22. J. Carstensen, R.Prange, H. Föll: ECS meeting San Diego 1998, this proceedings

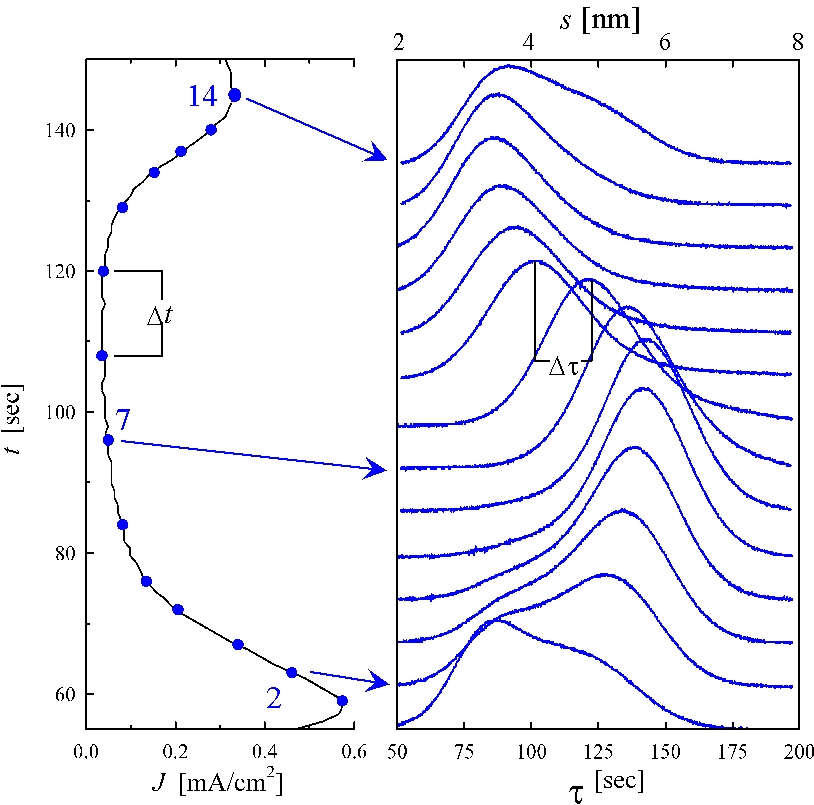
Fig. 1: a) The oscillating current density J as a function of time t applying a voltage of 4.5 V vs. SCE. Electrolyte is 0.1w% HF + 1 M NH4Cl (volume ratio: 1:1), pH 2.8. b) Transient currents after reducing the potential to open circuit potential at several phases of the oscillation (indicated by the arrows) as a function of time t.

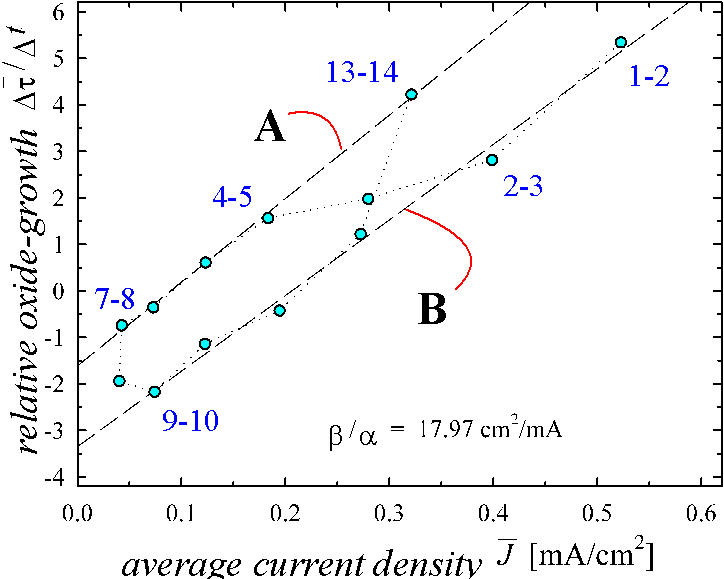
Fig. 2: Plot of the experimental results using Eq. (9). Line A and line B are calculated from a linear regression. Line A displays the correct values for the enhanced dissolution rate =1.7 and the dissolution rate a=0.04 nm/sec. Line B shows an offset, corresponding to the missing suboxide charges as outlined in Fig. 3.

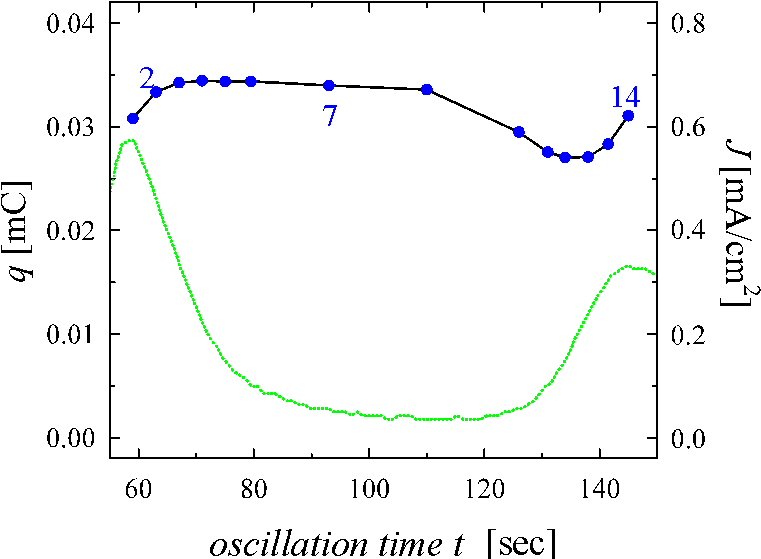
Fig. 3: Current oscillations (dotted line, same as Fig. 1a) and total charge (solid line) released at various phases of one oscillation as obtained by integrating the current transients.

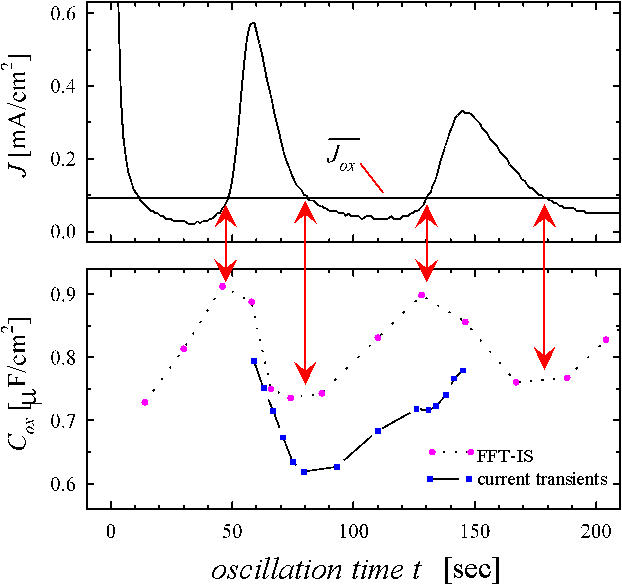
Fig. 4: a) Current oscillations (same as Fig. 1a) and the mean oxidizing current. b) Measured capacitance (dotted line, FFT-IS) and calculated capacitance (solid line, current transients) using Eq. (13). The arrows point to the calculated maxima and minima of the capacitance.