A NEW VIEW OF SILICON ELECTROCHEMISTRY
H. Föll, J. Carstensen, M. Christophersen, and G.
Hasse
Materials Science, Faculty of Engineering
Kaiserstr. 2, 24143 Kiel, Germany
Phone: + 49 431 77572-501
Email: hf@tf.uni-kiel.de
The salient features of the current burst model for the Si – electrolyte interface is presented in a short overview. In the current burst model, charge transfer at the Si – electrolyte interface is localized in space and time and intrinsically stochastic; all phenomena encountered in Si electrochemistry then are manifestations of the nucleation probabilities for current bursts, which depend on the system parameter in an unambiguous way. One of the unique features of the model is the existence of an internal time constant (equal to the average duration of a current pulse) which ultimately is the reason for the observed oscillations of the current in time and in space – the latter case describing pores. For pores, the intrinsic time constant is expressed as an intrinsic length scale which is determined by the interaction of current bursts within the same cycle, i.e. by the size of synchronized domains. The pore morphology is the result of the interaction of the intrinsic length scale with external length scales, e.g. the space charge region depth; smooth macropores are obtained when the relevant length scales are similar. The existence of an intrinsic time constant and length scale will be demonstrated by resonance phenomena which were observed for the first time in pore growth.
The electrochemistry of Silicon has proved to be a rewarding but challenging research field. Applications of many kinds keep appearing or are announced [1 - 6], but many features, especially anodic dissolution, are still not well understood. The formation processes governing the increasing number of specific pores (see, e.g., [7 - 9]) are the most prominent example, but other features of the anodic dissolution of Si can be just as puzzling. Most prominent are the current-voltage oscillations [7, 10, 11], but it should also be kept in mind that even something as "simple" as the basic IV-characteristics of a given electrochemical Si system is not yet predictable.
It appears that Si-electrolyte systems contain critical points in parameter space. Examples are the sudden disappearance of the microporous layer if the current (or the voltage) exceeds a critical value, the onset of oscillations, the sudden disappearance of oscillations with increasing temperatures [12] the switch from the <100> direction as the preferred growth direction for macropores to
<113> if a critical angle in the substrate orientation is exceeded [13, 14], but also – and this is already a prediction of the current burst model – the switch from macropores to micropores in the low current density region of Si – aqueous electrolyte systems.
Manifestations of this kind are typical for "critical systems" [15] (connected to phenomena like phase changes, bifurcation, chaos, or self-organization) and generally require stochastic behavior (in space and time) of some elementary event. If the Si-electrolyte system is indeed a critical system, a stochastic element then is needed in its description and the "current burst" model attempts just this.
The current burst model advocated in this paper is a generalization of a stochastic model used with some success to explain the current-voltage oscillations in the Si-HF system [11, 16]. Here it will be presented in a general way emphasizing the basic ideas; a more formal treatment will be given in [11, 16]. In what follows, we will briefly describe the oscillation model, give some general reasons for its extension to the whole of parameter space, specify the model in some detail and finally apply it to some specific observations concerning Si electrochemistry.
Current oscillations of the Si electrode could be explained in great detail [11] by postulating i) local current bursts through a closed oxide lasting a short time and ii) interactions (in space) between current bursts above a critical potential. The (macroscopic) phenomena observed are averages over the effects of many current bursts, but fully determined by the nucleation and interaction of individual current bursts.
A local current burst in the "oscillation regime" (closed oxide layer is present) is a charge transfer process localized in space and time; it nucleates whenever the local oxide thickness (which decreases continuously because of the dissolution in HF), becomes small enough. During the current burst the prevalent reaction is oxidation, as a result of a current burst an oxide "bump" is produced; the process stops when the decreasing field strength (because of the net oxide growth) can no longer drive a current through the oxide. Eventually, a new current burst will nucleate – somewhere and sometime.
Interactions in space between current bursts occur because a newly nucleated current burst in the neighborhood of another one will have to grow less oxide before it turns off – the oxide "bumps" overlap to some extent. The turn-off event thus couples to next neighbors if they are close enough, and this means that local physical interactions in space cause correlation in time between individual current bursts.
With an increasing number of current bursts, the interaction in space increases and thus the strength of the correlation increases, too. At some critical point a percolation threshold is reached, and the correlation spreads to many current bursts – we have the onset of a large-scale synchronization and current oscillations are observed in the external circuit.
Below that threshold, many domains are formed that contain synchronized bursts, but are not synchronized with each other. The average size of these domains is still determined by percolation and an unambiguous (albeit complex) function of the system parameters; it defines an intrinsic length scale of the system.
Monte Carlo simulations of this model with relatively few assumptions [11] could not only reproduce all observed features of (slow) oscillations in great detail (including not only the current oscillations, but also the oscillation of the oxide thickness, the oxide roughness, the current transient spectra, the capacity of the system and the oscillations of the apparent dielectric constant), but made predictions: Even at voltages (or current densities) below the percolation threshold needed for macroscopic current oscillations, the current oscillates locally because of the current bursts. Without large-scale synchronization, however, this would only be detectable in the noise spectrum, a prediction that has been verified in the meantime [17].
In conclusion, current bursts must exist outside of the (macroscopic) oscillation regime, too - at least as long as the surface is completely covered with oxide. In a sweeping generalization of the oscillation model, we next assumed that current always flows by current bursts, i.e. by a stochastic process in space and time. The consequences of this hypothesis proved to be attractive: With some assumptions concerning the nature of the current bursts outside the oscillation regime of the IV-characteristics, pore formation appeared not only to be comprehensible, but many predictions resulted, some of which were verified in the meantime. In addition, measurements from impedance or transient spectroscopy could be interpreted most easily in terms of current bursts.
The wealth of phenomena observed in Si - electrolyte systems cannot possibly be explained by a simple equation or description of the processes. For lack of space, we must look at the current burst model in a somewhat dogmatic manner; neglecting complications. We only include some assumptions that are either dictated by logic or necessary to understand outstanding pertinent features of pore etching (e.g. the anisotropy).
A current burst in its most general form consists of a series of charge (Qi) and time (ti) consuming processes (Fig. 1).
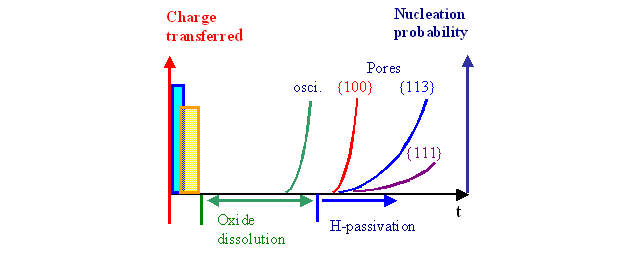 |
Fig. 1 |
The charge transfer starts with direct dissolution, followed by oxide formation. This is required because an oxide "bump" quenches current flow; direct dissolution thus could not appear after the oxidation. The time for charge transfer is short. Next, the oxide must be dissolved, which takes a comparatively long time. Under conditions of a closed oxide layer (i.e. in the oscillation regime), a new current burst will nucleate with increasing probability whenever (and wherever) the oxide thickness is going down. This describes the system kinetics in the oscillation regime as outlined before.
At lower potentials/current densities, the oxide may be completely removed before a new current burst is nucleated. In this case the Si surface starts to "passivate" by H-coverage, a relatively slow process with a strong intrinsic anisotropy. This means that in ideal conditions (e.g. clean surfaces exposed to H2 under UHV) {111} surfaces passivate fastest, {100} surfaces slowest [18]; and this behavior may be modified to some extent by the electrolyte.
Passivation in this context means the removal of mid-gap states; with progressing degree of passivation, Fermi-level pinning thus disappears, a space charge region develops, and the potential at the interface decreases. The essential point is that the probability for current bust nucleation decreases with increasing passivation – it follows that there is a strong tendency to nucleate new current bursts on {100} surfaces.
The average current iCB transferred during a current burst is by necessity iCB=å Qi /å ti . It follows:
- The charge consuming processes and the time consuming processes are (almost completely) decoupled. The duration of a current burst thus is mostly determined by the chemical processes, with oxide dissolution dominating.
- A given system therefore has an intrinsic time constant defined as the average time between two current bursts. This is a unique feature of the current burst model and will be of prime importance later on. Since time scales are transferred to length scales via the percolation process synchronizing next neighbors, the very long time constant of the oxide dissolution is the lever that transfers microscopic events on the nm current burst scale to macroscopic scales of µm.
- The average current density of a current burst (in a given system) is relatively constant with respect to the applied voltage and equal to jPSL. This is not only suggested by suitable measurements [19], but may be qualitatively understood: The direct dissolution part of the current burst enables oxidation in a second step – more dissolution produces more surfaces which allows more oxidation. More oxide takes longer to dissolve: å Qi /å ti stays (about) constant! The equality to jPSL means that current bursts define jPSL as the maximum current density that a given surface – completely covered with CBs – can carry. Note that this implies that increasing the current will increase the average number of active current bursts (and thus "porosity") and that the intrinsic time constant of the system is not constant with respect to the voltage.
A first essential feature of the current burst model is that all manifestations of electrode behavior now depend exclusively on when and where current bursts nucleate. Correlation in time produce current oscillations, correlation in space produce pores – by necessity! This is illustrated schematically in Fig. 2.
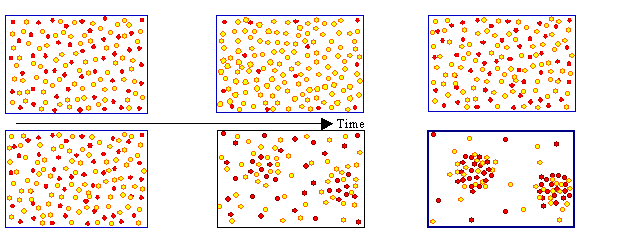 |
Fig. 2 |
Correlation in space is produced by interactions in time which means that the nucleation probability of a current burst depends on what happened before. Since the nucleation probability is larger for smaller degrees of H-passivation, and H-passivation in turn is minimal on the {100} surfaces just after the oxide is removed, there is an automatic coupling of new current bursts to old ones in the "pore regime" (i.e. whenever free Si surface is present) – the interaction in time is an intrinsic feature of the model. Whereas this is a necessary ingredient for the clustering of current bursts and thus the appearance of (meso- or macro) pores; it is not totally sufficient: At low current densities for example, the number of current bursts nucleating per time unit may still be larger somewhere in a large area having a small nucleation probability, compared to the small area around an "old" current burst having a large probability, because the number of current bursts nucleating is probability times area. This allows for micropores, otherwise only macropores would be observed.
It is also not possible at this point to make any general statements about the size of the current burst cluster which defines the pore diameter. This is not unlike the situation in, for example, the Fe – C system (i.e. steel), where everything that can possibly happen is contained in the Fe-Fe, Fe-C and C-C interactions. It may be easy to predict that C will precipitate in certain circumstances, but no statement whatsoever can be made about the size of the precipitates without additional knowledge.
Additional knowledge about current bursts comes from considering the response of the direct dissolution part and the oxidation part of a current burst to system parameters and the consequences for the evolution of the system – how pores are formed and grow. This is the complicated part. In an on-going interplay of experimental observations, interpretations in terms of the current burst model, predictions, experimental checks, and theoretical considerations, the following features emerged:
The direct dissolution part of a current burst has the following properties:
- Strong preference for nucleation on {100}; never observed on {111}.
- Valence n of 1 – 4; typically around 2. This means direct dissolution makes "best" use of available holes; but 4 – n holes must be supplied by the chemistry of the system (by electron injection). The maximum current possible thus is limited by the chemistry of the system.
- Opens the way for the energetically preferred oxidation reaction (the end product of the process is always SiO4!) which then quenches direct dissolution.
- Preferred reaction at high field strength (including carrier generation by avalanche effects), lack of holes (relative to the number that could be "used up" at the interface), or lack of reactive oxygen in the system (e.g. in acetonitrile).
- Preferred reaction at high field strength (including carrier generation by avalanche effects), lack of holes (relative to the number that could be "used up" at the interface), or lack of reactive oxygen in the system (e.g. in acetonitrile).
- Responds to changing the H kinetics (e.g. by adding protonizers as, e.g. [20])
- If dominant, produces "dendritic pores" (or "break-through pores", "fractal pores", mesopores,...); a paradigmatic example is shown in Fig. 3.
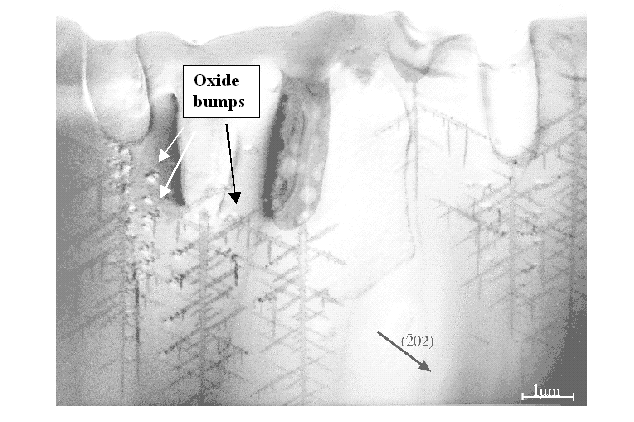 |
Fig. 3 |
The oxidation part of a current burst has the following properties:
- Rather isotropic process (would result in electropolishing by itself).
- Valence n=4; i.e. totally dependent on hole supply from Si. Maximum current possible depends on oxide dissolution kinetics; i.e. HF concentration (and temperature).
- Self stopping (for j < jPSL) because of the oxide produced in a burst.
- Driven by electrochemistry, i.e. potential at interface.
- Preferred reaction at high potentials and surplus of holes if sufficient O- is available.
- If strong compared to direct dissolution, produces "macropores" with not very pronounced directionality; a paradigmatic example is shown in Fig. 3.
Macropores are formed if the direct dissolution part and the oxidizing part of a current burst are balanced within some limits depending on the system. If the system looses this balance because, e.g., the supply of holes (or reactants) decreases, a critical point may be reached where the pore morphology changes suddenly. One example is shown in Fig 3, where pores in n-type Si are imaged by TEM. The competition between originally nucleated pores for the available holes leads to "winners" and "losers"; the effect is self-amplifying. The loosing pores experience a continuously decreasing hole supply which leads to a decrease of the oxidizing component. At some point a sudden transition occurs, because the oxidation "rearguard" can no longer keep in step with the direct dissolution "vanguard" (or, to put it bluntly, electropolish the fractals of direct dissolution), the pore morphology switches from smooth to dendritic. The oxidation component, however, is still present and powerful enough to quench the charge transfer in a burst. This is directly visible in parts of the picture, where oxide bumps are depicted as black-white contrasts by their strain field [21].
In what follows, some known facts will be interpreted in the framework of the current bust model and some new experiments, based on predictions, will be presented. The first topic are macropores in p-type Si which are observed either with aqueous electrolytes at very low current densities, or in organic electrolytes typically minimizing oxidizing components (e.g. by avoiding H2O) [20, 22 - 25]. It is clear from experiments that macropores of all sizes and shapes can be obtained, Fig. 4 shows some examples.
 |
Fig. 4 |
Note, that the morphology of pores obtained in totally different electrolytes can be quite similar, and that it is possible to obtain uniform macropores rivaling the "best" pores in backside illuminated n-type Si. This is remarkable because all the ingredients thought necessary for uniform macropores (e.g. backside illumination and carrier focussing on the pore tip) are not present in this case.
Suffice it to say that in the current burst model there is no principal difference between n-type and p-type Si – macropores in p-type Si thus are nothing special. The density and type of available carriers is but one parameter influencing the nucleation of current bursts (albeit with profound consequences), but the general principle of interaction between current bursts and the resulting correlation is the same. It has been shown that by adjusting the balance between direct dissolution and oxidation (by adding oxidizers or protonizers to the electrolyte), the pore morphology changes in accordance with the rules given above and that pores morphologies can be optimized [20].
Next, the results of an experiment based on a prediction of the current burst model concerning the generation of macropores in highly doped n-type Si will be discussed. So far, only mesopores have been observed at high doping levels, and according to the current burst model this must be caused by too much direct dissolution. The reason for the lack of oxidation must be sought in the relative shortage of holes in this case, which tips the balance to direct dissolution. This seems somewhat contradictory because highly doped Si seems to offer more carriers (in p+-Si directly, in n+-Si via easy avalanche effects) than regular Si. Whereas this is true, increasing the carrier density also decreases the space charge region; as a result the potential at the interface goes up (less voltage drops in the space charge region). Since the number of holes that could be consumed in the electrochemical process of oxidation grows with exp(U/kT), increasing the doping actually leads to an undersupply of holes relative to what could be utilized, and the oxidation part decreases.
If that is true, the situation might change if the oxidizing power of the electrolyte is strengthened and macropores might form if oxidizers, as e.g., H2O2 or CrO3 are added to the electrolyte. The experiment showed [26] that there is indeed a small window for macropores at the right conditions: Fig. 5 gives an example.
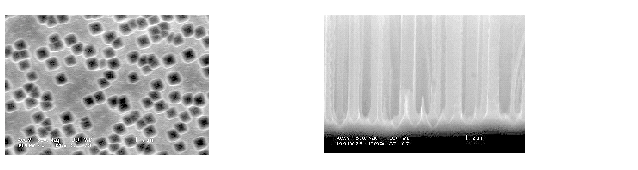 |
Fig. 5 |
Generally, the current burst model proved to be very helpful for designing and interpreting experiments, including I-V-characteristics, current transient and impedance spectroscopy; some results are reported in detail in [17, 20, 26, 27], but here just one more feature shall be discussed: The impact of the intrinsic time constant inherent in the current burst model as mentioned before.
So far, pores were discussed as a consequence of current bursts correlated (or synchronized) in space; it was implicitly assumed that there is no correlation in time. There is, however, no particular reason why correlation in time should not occur, the domains mentioned earlier are the result of such a correlation The formation of sidepores at relatively constant intervals is often observed; this may be seen as a correlation in time: In regular time intervals the current bursts at the pore tip are more active and sidepores are formed. It is important in this context to realize that sidepores do not nucleate at the pore wall and grow independently from what happens at the pore tip, but nucleate at the pore tip and branch off as the pore grows.
Exactly how a partial synchronization in time is achieved via percolation effects is open to speculation, but the general interpretation allows a very specific prediction. If general rules about the behavior of stochastic (or critical) systems apply to the current burst model (as they should), it can be expected that modulations of external parameters with a frequency that is tuned to the reciprocal value of the ntrinsic time constant of the system (which, for current bursts, is approximately given by the oxide dissolution kinetics, cf. chapter 3), will lead to resonance effects and thus to a forced synchronization of the system. The system then should be less chaotic and much more homogeneous in its outward appearance.
To test this prediction in an experiment, conditions leading to the most "chaotic" macropores ever observed were chosen [28]: n-type Si, illuminated from the backside, in an organic electrolyte (dimethylformamide). The current I was given by I=I0 + Imsin(ft); Im was 20% of I0. The result of this experiment is shown in Fig. 6. – perfect synchronization is definitely achieved at 33 mHz.
 |
Fig. 6 |
Similar results are obtained for different systems; in all cases the existence of an internal time constant of the system tied to the oxide dissolution kinetics was found. As a practical result, it is now clear why macropores often showed a peculiar and strongly non-linear response to modulations of the external parameters [29] and how the experimental conditions should be chosen to obtain optimal results.
The experiments not only support the current burst model and open the way to systematic and quantitative studies of the details, but allow a more general interpretation of pore formation since it also demonstrates that the intrinsic time constants of the system are expressed as intrinsic length scales in the pore morphology. In particular, the very long time constant of oxide dissolution is the decisive factor for the large length scales of macropores. There are, however, more length scales that may influence the system dynamics. To name just a few (with very rough numbers): quantum wire effects (nm scale), avalanche break-through (10 nm scale), space charge region (10 nm - 10 µm), Helmholtz layer thickness (nm), stability of diffusion (µm – cm). "Perfect" macropores are achieved if the dominating length scales are similar, complicated morphologies result if they are incompatible.
As stated before, pores are an inherent feature of the current burst model because of the interaction in time between bursts, but no statement about the size of pores could be made. That statement is now possible: The size (and morphology) of pores is given by the dominating length scales of a particular system. As a corollary, the current burst model is generally compatible with the many pore formation models proposed earlier [8, 22 – 24, 30 - 38]; because, in a general way of speaking, earlier models essentially discussed some of these length scales for special cases.
There is little doubt in the opinion of the authors that the current burst model has the potential to explain most if not all phenomena encountered in Si electrochemistry. Whereas some details are still vague and parts of the model are only qualitative, there is a clear potential for its development into a quantitative theory. Specific experiments – including pore etching, transient and impedance spectroscopy, but also new techniques (in this context), as, e.g., noise spectroscopy or in-situ micro-analytical tools – will provide basic data, whereas theoretical evaluation in the context of stochastic physics will provide the frame work. The reward may not only be a much better understanding of the solid-liquid interface dynamics, but better technological uses of pore etching, e.g. in the context of photonic crystals [6].
The authors are indebted to Dr. Popkirov for designing and building special hardware and for stimulating discussions. Dr. Bob Falster (MEMC) and Dr. W. Zulehner (Wacker Chemitronic), as always, could be relied upon to supply Si, in particular with unusual properties; this is gratefully acknowledged. Parts of the work reported was supported by the DFG (Förderungsnummer: FO 258/1-2)
[2] P. Kleinmann, J. Linnros, S. Petersson, Mat. Sci. Eng., B 69 – 70, 29 (2000)
[3] R. Angelucci, A. Poggi, L. Dori, A. Tagliani, G. C. Cardinali, F. Corticelli, M. Madisaldi, Journal of Porous Materials, 7, 197 (2000)
[4] K. Imai, Solid State Electron., 24, 159 (1981)
[5] V. Lehmann, W. Hönlein, H. Reisinger, A. Spitzer, H. Wendt, J. Willer, Solid State Technol., 38, 99 (1995)
[6] F. Müller, A. Birner, U. Gösele, V. Lehmann, S. Ottow, H. Föll, Journal of Porous Materials, 7, 201 – 204 (2000)
[6] T.M. Benson, H. F. Arrand, P. Sewell, D. Niemeyer, A. Loni, R. J. Bozeat, M. Krüger, R. Arens-Fischer, M. Thönissen, H. Lüth, Mat. Sci. Eng., B 69 – 70, 92 (2000)
[7] H. Föll, Appl. Phys. A, 53, 8-19 (1991)
[8] V. P. Parkhutik, in Porous Silicon, 1st. ed., Z. C. Feng und R. Tsu, Editors, p.301, World Scientitic, Singapore (1994)
[9] G. Cullis, L.T. Canham, P. D. J. Calcott, J. Appl. Phys., 82 (3), 909 (1997)
[10] F. Ozanam, J.-N. Chazalviel, A. Radi, M. Etman, J. Electrochem. Soc., 139, 2491 (1992)
[11] J. Carstensen, R. Prange, H. Föll, , J. Electrochem. Soc.,146, 1134 (1999)
[12] V. Parkhutik, E. Matveeva, R. Perez, J. Alamo, D. Beltrán, Mat. Sci. Eng., B 69 – 70, 553 (2000)
[13] S. Rönnebeck, S. Ottow, J. Carstensen, H. Föll, Journal of Porous Materials, 7, 353 (2000)
[14] S. Rönnebeck, S. Ottow, J. Carstensen, H. Föll, J. Electrochem. Soc. Lett., 2,126 (1999)
[15] D. Stauffer, A. Aharony, "Introduction to Percolation Theory", Taylor & Francis Group, Basingstoke House, United Kingdom (1995)
[16] J. Carstensen, R. Prange, G. S. Popkirov, H. Föll, Appl. Phys. A., 67, 459 (1998)
[17] G. Hasse, J. Carstensen, G. S. Popkirov, H. Föll, Mat. Sci. Eng. , B 69 – 70, 188 (2000)
[18] K. W. Kolasinski, Int. J. Mod. Phys., B9, 2753 (1995)
[19] V. Lehmann, J. Electrochem. Soc., 140, 2836 (1993)
[20] M. Christophersen, J. Carstensen, A. Feuerhake, H. Föll, Mat. Sci. Eng., B 69-70, 194 (2000)
[21] C. Jäger, B. Finkenberger, W. Jäger, M. Christophersen, J. Carstensen, H. Föll, Mat. Sci. Eng., B 69-70, 199 (2000)
[22] E. K. Propst, P. A. Kohl, J. Electrochem. Soc., 141, 1006 (1994)
[23] E. A. Ponomarev, C. Levy-Clement, J. Electrochem. Soc. Lett., 1, 1002 (1998)
[24] R. B. Wehrspohn, J.-N. Chazalviel, F. Ozanam, J. Electrochem. Soc., 145, 2958 (1998)
[25] V. Lehmann, S. Rönnebeck, J. Electrochem. Soc., 146, 2968 (1999)
[26] M. Christophersen, J. Carstensen, H. Föll, this proceeding (2000)
[27] G. Hasse, M. Christophersen, J. Carstensen, H. Föll, this proceeding (2000)
[28] M. Christophersen, J. Carstensen, H. Föll, this proceeding (2000)
[29] J. Carstensen, G. Hasse, M. Christophersen, H. Föll, this proceeding (2000)
[30] M. J. J. Theunissen, J. Electrochem. Soc., 119, 351 (1972)
[31] V. Lehmann, H. Föll, J. Electrochem. Soc., 137,653 (1990)
[32] M. C. dos Santos, O. Teschke, J. Vac. Sci. Technol. B, 16 (4), 2105 (1998)
[33] R. L. Smith, S. F. Chung, S. D. Collins, J. Electron. Mater., 17, 533 (1988)
[34] Y. Kang, J. Jorne, J. Electrochem. Soc., 140, 2258 (1993)
[35] Valance, Phys. Rev. B, 52, 8323 (1995)
[36] J.-N. Chazalviel, R. Wehrspohn, F. Ozanam, Mat. Sci. Eng., B 69-70, 1 (2000)
[37] V. Lehmann, R. Stengl, A. Luigart, Mat. Sci. Eng., B 69-70, 11 (2000)
[38] V. Lehmann, U. Gösele, Adv. Mat., 4, 114 (1992)