A model for current oscillations at the Si-HF-System based on a quantitative analysis of current transients

J. Carstensen, R. Prange, G.S. Popkirov, H. Föll

Lehrstuhl für Materialwissenschaft, Technische Fakultät der Universität Kiel, Kaiserstraße 2, D-24123 Kiel

(Fax: (+431) 77572-503, e-mail: jc@tf.uni-kiel.de)

Abstract

Applying sufficiently large anodic potentials, the dissolution of silicon in fluoride electrolytes causes current oscillations which are correlated with an anodic growth of silicon oxide. The dynamics of oxide growth and dissolution is studied by transient current measurements at various phases of the oscillation. An interpretation of the transient currents as a direct representation of the oxide thickness distribution allows the calculation of the oxide capacity, showing excellent quantitative agreement with in situ FFT impedance measurements. The analysis of an averaged continuity equation yields absolute values for dissolution rate and oxide thickness and provides components for an oscillation model.

The physical character of local oscillators on a nm scale will be outlined. Next neighbor coupling leads to percolation areas of about 100 nm as result of Monte Carlo simulations. The percolation provides an intrinsic synchronization mechanism leading to macroscopic oscillations.

PACS: 64.60.Ak, 68.45.-v, 82.40.-g, 82.45.+z, 82.65.-i

1. Introduction

Silicon electrodes in fluoride containing electrolytes exhibit a number of interesting phenomena, including micro-, meso-, and macro- porous silicon formation, electropolishing and current-voltage oscillations [1, 2, 3].

Independent of the doping, current- as well as voltage-oscillations are observed. While results of voltage oscillations are published rarely [4], a number of papers deals with the investigation of current oscillations, which are supposed to be strongly coupled to the growth of the silicon oxide on the surface of the electrode. In situ analysis with ellipsiometry [5, 6, 7], IR-spectroscopy [8, 9], microwave reflectivity [10], atomic force microscopy [11] have been performed in order to obtain information on the thickness and the morphology of the oxide layer as a function of the oscillation phase, and thus to examine the dynamics of the oxide growth and dissolution.

Gerischer [12] emphasized that the migration of the ions through the oxide is the key for understanding the oscillations. A model of local oscillators externally synchronized in order to get macroscopic oscillations has been discussed by Chazalviel et. al. [13, 14], but up to now, no microscopic model has been presented.

Measurements of the current transients after changing the anodic potential to open circuit potential are a valuable tool for obtaining data on the oxide present at different phases of the oscillation; results have been presented by [15] relating to the oxide thickness and its homogeneity at different phases of the oscillation. In this paper we discuss a quantitative interpretation of the current transients and apply it to our own data, which allows us to quantify parameters as.e.g. dissolution rates, oxide thickness, distribution function of the oxide thickness, and the capacitance of the oxide, in full agreement with the measurements. Since the model is somewhat complicated, we will proceed by making a number of simple assumptions, some of which will only be justified and/or modified at a later stage of the discussion.

In a second part of the paper, the first fully consistent model of current oscillations is presented, including sone quantitative results. Monte Carlo simulation using this model point to a percolation mechanism as the cause for the long-range synchronization of local oscillators. The percolation defines a length scale of about 100 nm for synchronized areas, which is in good agreement with AFM-studies by

2. Experimental setup

The experiments were performed with {100} oriented p-Si wafers of 1 Wcm resistivity. Ohmic contacts were provided by p⁺-doping of the back side. The samples were etched in diluted HF solution to remove the native oxide layer.

The electrochemical cell was made of PVC with an active electrode area of 0.3 cm². The counter electrode was a Pt grid. The reference electrode was a saturated calomel electrode (SCE) connected to the cell by means of an Agar-Agar bridge with a Luggin capillary mounted close to the working electrode surface.

The electrolyte was a solution of 0.1 w%HF and 1 M NH₄Cl (volume ratio: 1:1, pH 2.8) and was circulated through the cell by a peristaltic pump.

The current-time and in situ FFT-impedance spectroscopy (FFT-IS) measurements were carried out using a home made potentiostat and FFT-impedance spectrometer as described in more detail in [16, 17].

3. Transient Currents Measurements and Their Quantitative Interpretation

Applying a potential of 4.5 Volt vs. SCE leads to slow current oscillations as shown in Fig. 1a. These oscillations with a frequency f < 0.02 Hz are well reproducible and allow the investigation of the current transients as described e.g. in [12, 15, 18, 19]. At several stages of the oscillation the potential is stepped to open circuit potential, i.e. the potential , for which the current i is zero in a steady state. Subsequently the current is measured as a function of time. In addition in situ FFT-IS measurements were performed during the current oscillations. The current-time curves in Fig. 1b contain information about the oxide layer as discussed in [15]. The shape of the transient current changes with the phase of the oscillation and will be analyzed in detail in the following.

Under open circuit condition the surface oxide is chemically dissolved, reducing the local thickness of the oxide layer s(x,y,t) with the velocity ds/dt=-a, which is assumed to be constant. Reaching the sub-oxide layer a current occurs due to the dissolution of the substoichiometric composition of the oxide layers near the bulk silicon [12, 15, 19]. The current transients have been discussed qualitatively by [15] to describe the inhomogeneity of the oxide thickness as a function of oscillation phase. We suggest a new way of evaluating the transient currents which is based on simple assumptions and fully consistent (but independent of) the oscillations model discussed later.

With the following fundamental assumptions, a quantitative interpretation of the transient current curves is possible:

Assumption 1: All of the transient current is generated by the charge of the dissolving sub-oxide

Assumption 2: The released charge per unit area g for the sub-oxide layer is constant and independent of the phase of the oscillation.

Assumption 3: The time for dissolving the sub-oxide is small in comparison with the time for dissolving the oxide, which means that the thickness of the sub-oxide layer is small compared to the thickness of the oxide.

We will slightly modify assumption 2 later on, but at this stage they will suffice for a first analysis. If our assumptions are correct, each unit area with oxide thickness s adds a charge g at the time t=(s / a) to the transient current i(t). Thus i(t) dt =g D(s=at) ds with D(s) being the sum of all areas with oxide thickness s at t =0. In other words, D(s) is the thickness distribution of the oxide at any given point of the oscillation. In consequence, the transient current curves in Fig. 1b show the exact distribution of the oxide thickness at the phase of the oscillation where the transient current measurement was started. Fig. 1b therefore contains a thickness scale (top) in addition to the time scale (bottom); how the numbers are derived will become clear later on. In the current minimum of the oscillation (Fig. 1b; measurements 6-9), the peak width and therefore the distribution of oxide thickness D(s) is narrow, indicating that the lateral distribution of oxide thickness is quite homogeneous. In this phase the mean thickness is decreasing while the shape of the transient peak does not change significantly. This indicates a laterally homogeneous Ds of the oxide. The dissolution velocity a of a "static oxide" (an expression used to distinguish between the dynamically growing and dissolving "oscillating oxide" present during oscillations, and the passively dissolving "static oxide" present during the current transient measurements) thus can be obtained by calculating a=D s/D t, or D s=a D t .

First conclusions can be drawn: In the current minimum of the oscillation (Fig. 1b: measurements 6-9) the peak width and therefore the distribution of oscillating oxide thickness D(s) is narrow, indicating a relatively homogeneous lateral distribution of the oscillating oxide thickness. In this phase the mean thickness is decreasing while the shape of the transient peak does not change significantly. This indicates a laterally homogeneous dissolution of the oscillating oxide.

In contrast, the measurements 1-3 show two peaks; a decreasing one for areas with thin oxide and a growing peak for areas with thick oxide. This obviously describes the growth phase of the oscillating oxide, which correlates well with the maximum in the oscillation current. It suggests that at in some areas of the sample, the oxide surface is still dissolving, while in other areas the oxide thickness is growing. This calls for an inhomogeneous lateral distribution of oscillating oxide thickness during the high-current phase of the oscillation. The lateral dimension of the areas with thin and thick oxide can not be deduced directly, we will come back to this later.

It should be noted that our interpretation is somewhat different from other views of the transient current, e.g. [19, 20, 21] the difference is, however, not as large as it seems, because we make no assumptions of the origin of the current. Within our model it does not matter if charge carries come from the Si-O bond, from H-termination or whatever. Assumption 2 only ascertains that charge is released as soon as the Si - SiO₂ interface is reached and that it is always the same amount per area. We will not justify this assumption directly, but via the general predictive power of our model.

Recognizing, that the current peak during oscillation coincides with the growth of the oscillating oxide, we add a fourth assumption for a first quantitative analysis:

Assumption 4: All of the current builds up oxide.

This assumption must not be generally true, but only for the "low-frequency" oscillations, obtained, e.g. at very low HF concentrations, discussed in this paper.

In the phase, when least oscillation current is measured (Fig. 1b: e.g. measurement 8-9) the overwhelming reaction then must be chemical etching of the "oscillating oxide". The time interval between measurement 8 and 9 is Dt = 12 sec according to Fig. 1a. During this time interval only dissolution of the "oscillating oxide" takes place. Its thickness decrease, as measured with evaluating the transient currents, was Ds=a D t=a · (20 sec) according to Fig. 1b. However, Ds can also be obtained from looking a the time interval between the two transient current measurements, it must also been given by Dt, with being the chemical dissolution rate of an "oscillating oxide" in the phase of little current flow. Putting both relations together, we obtain for the (obviously enhanced) dissolution rate of an "oscillating oxide" in the non-growth regime

=(Dt / Dt) a=1.7 a.

It is easily verified that all data points in the "non-growth regime" of the oscillating oxide (roughly points 6 - 9) would yield the same value. Evidently, we have to consider two different dissolution velocities: a corresponds to the chemical dissolution of a "static oxide" when open circuit potential is applied and no current is flowing, is the dissolution rate of an "oscillating oxide".

There may be several reasons for this increased dissolution rate, e.g. a potential dependence of the oxide dissolution rate or a roughening of the oxide surface, leading to an increased effective surface of the "oscillating oxide". As will be shown later, the factor 1.7 is nearly independent of the oxide thickness, and thus not dependent on the electrical field in the oxide, which prompts us to consider an increased (and always maintained) roughness of the oscillating oxide as the prime source of the dissolution enhancement.

Inherent in the above assumptions is a local continuity equation, which will be formulated and developed. For each point of the "oscillating oxide" the net growth rate per unit area is

(2)

J_ox is the current density, is parameter determined solely by the geometry and the valence of the SiO₂ building process, and is now, more generally, the effective dissolution rate of the "oscillating oxide" at any point in time or space.

Eq. (2) can not be proved experimentally, because it is impossible to measure the parameters ds/dt, J_ox and as a function of location and time directly. But since we can extract for each transient current measurement i the change of the "oscillating oxide" thickness between time t_i and t_i+1 and the average current density for this interval from the oscillation current, we use Eq. (2) in an integral form.

For a quantitative description of an inhomogeneous oxide layer, which is build up by a current varying in time and location and dissolved by a laterally inhomogeneous dissolution rate, we must integrate Eq. (2) in space and in time. The integration over the inhomogeneous oxide layer yields for the average oxide growth rate

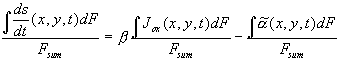, (3)

with .

For the quantitative analysis of the transient current, we need the change of the average "oscillating oxide" thickness between two measurements at time t_i and t_i+1. Using Eq. (3) we find

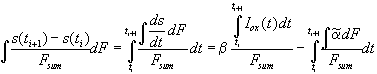. (4)

We define a mean dissolution rate 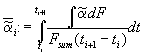. (5)

Taking into account the interpretation of the transient current to be the distribution function of the oxide thickness s =a t, we calculate the mean oxide thickness

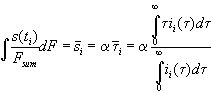, (6)

i_i(t) is the transient current of measurement No. i.

Our fourth assumption that the total oscillation current generates oxide, allows to calculate the mean current used for building up oxide between two measurements of the transient current

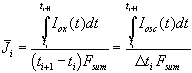. (7)

Including Eq. (5) - (7) into Eq. (4) we get the simple and new result

. (8)

Despite of the fact, that Eq. (8) contains a number of integrals, it displays the same physical meaning as Eq. (2), but now all important quantities can be computed from measured data. If is constant and our assumptions are correct, a linear relation between the measurable parameters / D t_i and is predicted for any pair of measurements of the current transients.

Before applying Eq. (8) to our measurements, we will evaluate the integral , which yields the total charge of the sub-oxide layer and which so far was assumed to be constant. This can be checked experimentally by integrating numerically the current transient curves, Fig. 2 shows the result. Obviously, the total charge is not constant within the oscillation period. While the oscillation current is small, the charge has its maximum value and is approximately constant. This result violates our fundamental assumption 2, if taken on face value. There are at least three possible answers for the reduction of the overall sub-oxide charge: a) the charge per unit area in the sub-oxide layer is not constant and depends on the phase of the oscillation; b) there are regions without oxide and therefore without sub-oxide in certain periods of the oscillation; c) for parts of the oxide layer, sub-oxide charge is not present or does not contribute to the current. Some strong arguments for the third interpretation will be discussed later in connection with the oscillation model.

Trusting the third interpretation this means to replace in Eq. (6) by its maximum value, which is the best value for the charge of the completely oxide covered area. We change Eq. (6) to

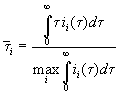. (6a)

With this correction as taken from the measurements is plotted against which, including the correction of Eq. (6a), is taken from the measurements, too, in Fig. 3. We emphasize that Fig. 3 shows exclusively experimental results, all that was done was to use the "recipes" given by Eq. [3] to [8] to process the raw data. Obviously most points are lying close to the two parallel straight lines, which have been calculated by a linear regression. Within one period of the oscillations the dynamic parameters change from one set, represented by line B, to a second parameter set, represented by line A, and (if the oscillation is undamped) return to line B. The representation of the data in this way therefore supplies a kind of phase-space with a closed cycle for an oscillating electrode system.

Eq. (8) predicted one straight line for of the processed data; Fig 3 gives us two - this needs discussion. We first consider line A. All points on these line correspond to the maximum charge in Fig. 2. or the "quiet" (=non oxide growing) phase of the oscillation. For we find, according to Eq. (8), , which coincides well with the independently obtained value of Eq. (1). We emphasize that the two methods, the investigation of the movement of the peak maximum using Eq. (1) and the calculation of the overall dissolution of the oxide with Eq. (8) are independent, but show the same enhanced dissolution of the "oscillating oxide", thus supporting our analysis. It should be mentioned that using in Eq. (6a) was an essential choice, otherwise we would not obtain the same value with both methods. Despite of the fact that the oxide thickness changes by a factor of two for the data points on line A, the enhanced chemical dissolution of the "oscillating oxide" is remarkably constant (otherwise no straight line would be obtained). As already mentioned above, this is a strong indication for an enhanced dissolution mechanism of the oxide that is independent of applied potentials.

The absolute value of a can be calculated from the slope of the straight line A, which is . Taking the parameter b=0.74 (nm/sec) · (cm²/mA) we find a=0.04 nm/sec. This is in excellent agreement with e.g. Sere et al. [21], who measured nm/sec as the dissolution rate of an anodic oxide grown in water.

Now we can calculate the absolute thickness by using Eq. (6), and the lateral distribution function D(s) of the oxide layer by multiplying the time axis in Fig. 1b with a. The thickness varies approximately from a minimum value of 2 nm to a maximum value of 7.5 nm. The lateral inhomogeneity or roughness is described by the differences of the oxide thickness at each moment. This value varies from roughly 6 nm at the maximum of oscillation current down to 3 nm in the minimum. The oxide surface hence is rather rough and this must lead to an enhanced dissolution - justifying our early interpretation. Again, we like to emphasize that a rough surface is obtained totally independent of any preferred interpretation for the enhanced dissolution rate, but gives a plausible explanation in hindsight. In conclusion, line A is what we expected to find with Eq. (8).

Line B needs some deliberation. It exhibits approximately the same slope as line A leading to the same value for a. But it shows a strong offset, which may have several reasons (all of them somewhat at variance with our four assumptions), e.g.: i) there is a current density component in J_osc, which does not build up oxide; ii) the dissolution of oxide is strongly enhanced in the period of the oscillation corresponding to the data points on line B; iii) there exist areas of the oxide, for which no sub-oxide charge is measured in the transient current peak. As discussed before, a nonoxidizing current and an electrochemically enhanced dissolution of oxide should depend on the oscillating oxide layer thickness. Since this thickness varies by a factor of two for the measurements on line B, resulting only in an offset between both lines, a potential dependent dissolution rate is rather unlikely. In addition, an enhanced dissolution rate by a factor 3.5 inherent in the offset, would be difficult to explain.

Thus we are again lead to believe that certain regions of a growing oxide do not show a sub-oxide charge. This assumption is in accordance with the results in Fig. 2 which show that some sub-oxide charge is missing when the oscillation current peaks. Including this interpretation into Eq. (8), a simple answer for the offset between both straight lines can be given.

For the mathematical description of the complete oxide area we introduce a distribution function L(s) in analogy to D(s) describing the areas with oxide thickness s, which do not add sub-oxide charge to the transient current. The correct mean oxide thickness is now calculated by

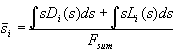. (9)

Defining 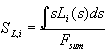, Eq. (8) is modified:

. (10)

The additional offset between the lines A and B of 1.7 in Fig. 3, if introduced in Eq. (10), yields

. (11)

Eq. (11) implies a constant growing rate of the L-regions during the high-current phase of the oscillations with a velocity h=1.7 a. The coincidence between the value of h and may be accidental, but it also be a hint on the dynamics of oxide growth which we do not yet understand.

We are now at a position to interpret the transient currents as an almost direct measurement of D(s), and this allows to predict physical parameters of the oxide layer which depend on its thickness. The most prominent candidate for this check is the oxide layer capacitance. The very slow oscillations observed for low HF concentration allow for in situ FFT-IS measurements. Fig. 4 displays the oscillation current density, the corresponding measured capacitance C_ox for the same sample as above, and the calculated capacitance. The measured value of C_ox is obtained from the raw FFT-IS data by fitting an equivalent circuit consisting of a parallel RC-circuit, C_ox and R_ox_,followed by a serial resistance R_ser; cf. [23] The calculated capacitance per unit area for the inhomogeneous oxide layer is given by

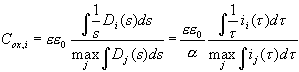, (12)

i.e. as a parallel connection of all oxide layer capacitance’s.

In evaluating this equation, we first try to understand the phase shift between the oscillation current density and the capacitance. We have found the oscillation to be a periodical change from a phase of growing oxide to a phase of decreasing oxide thickness. Since the capacitance increases when oxide thickness decreases and vice versa, we may expect the maximum and minimum of the capacitance, when the integral oxide thickness reaches its minima or maxima, respectively, i.e. . With Eq. (3) and using the constant value of , we find the corresponding current value 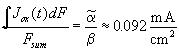. This value is also plotted in Fig. 4a. Whenever the oscillation current density equals this value, the phase changes from a period of growing oxide to a period of decreasing oxide thickness or vice versa. As predicted, at exactly this times the measured capacitance shows its extremas, being at minimum before the oxide thickness decreases and a maximum before the oxide thickness increases. This is a third independent check for the correct evaluation of the dissolution rate of the "oscillating oxide".

Taking e=3.9, which is the value for a thermal oxide, a=0.04 nm/sec as calculated before, and integrating the measured transient currents in Eq. (12), we obtain the theoretical capacity per unit area, which is plotted as a second curve in Fig. 4b. The bold vertical lines limit the range, corresponding to those points in Fig. 2, for which the full sub-oxide charge is measured. Only in this range the correct inverse oxide thickness is obtained when integrating . Comparing the measured and the calculated capacitance, we find an excellent agreement in all parameters. The steep slope before the minimum and a flat slope after the minimum are reproduced as well. The offset of about 10% for the absolute values of the capacitance is remarkably small, especially in view of the number of independent measurements needed to generate this data. The offset may even be explained by a slightly increased dielectric constant e for the anodic oxide compared to e of a perfect thermal oxide, which is rather to be expected.

We will now proceed to show that the "missing" sub-oxide charge in the high-current phase of an oscillation, which we encountered twice in interpreting the experimental data, is an inherent consequence of our oscillation model which will be presented next.

4. The Oscillation Model

The interpretation of the current transients as a representation of the distribution function D(s) of the oxide layer thickness s yielded quantitative data concerning the growth and dissolution of the oxide layer. In the following we use these transient current curves as a guide for a more detailed understanding of the current oscillation dynamics. In modeling the oscillation two essential ingredients are needed: a) a mechanism for localized oscillations on a small area of the electrode, and b) a mechanism to synchronize these local oscillators. In addition, not so obvious, a third ingredient is useful if not necessary, namely a desynchronization mechanism. Otherwise only strong oscillations or none at all will be obtained, whereas experimental results (incl., e.g. damped oscillations) call for a balancing of synchronizing and desynchronizing forces.

Full details of the model will be given elsewhere, here we concern ourselves with the basic mechanism and give some first results.

In a first step we discuss the dynamics of the localized oscillators, i.e. the mechanism of growing and dissolution of small (nm scale) oxide areas. In a second step, we suggest a synchronization mechanism which does not need an external triggering as has been postulated in [13]. In a third step, we implement the model in a Monte Carlo simulation and discuss some of the results obtained.

As already pointed out by several authors [12, 24], the transport of ions through the oxide layer is the key for the understanding of the oscillation phenomenon. For the extremely slow oscillations investigated in this paper, all of the oscillation current builds up oxide (assumption 4), so it is a direct measurement for the ion transport through the oxide. Looking at Fig. 1, the oxide growth starts when the oxide layer thickness s is small (measurement No. 10). Subsequently the measurements 11-14 (as well as 1-6 after closing the cycle) show an increasing area with thick oxide. The oxide growth stops at an upper limit of s. The broadness of the peak, in the oscillation current as well as in the transient current, is a measure for the synchronization of the oxide dynamics, i.e. not all oxide areas start to grow at the same time. Since the electric field across the oxide must be the driving force for the ion transport through the oxide, we assume that oxide growth starts when the electric field in the oxide approaches a maximum value E_max, corresponding to a minimum value of the thickness s_min. While the oxide thickness increases, the electric field decreases without reducing the ion transport through the oxide significantly. At a minimum value E_min, corresponding to a maximum value of the oxide thickness s_max, the oxide growth finally stops. This is the key assumption for our model of a local oscillator. Defining and (with, for the purpose of the Monte Carlo simulations, a reasonable probability distribution around these values), a model of an "ionic breakthrough" emerges. In analogy to an electronic breakthrough, we assume that after starting the ion transport through the oxide, the electric field can be reduced drastically without reducing the ion current. Leaving aside a microscopic picture for the ion transport and only pointing out that the ions have to pass a 2nm to 7.5nm thick oxide layer, a mechanism emerges centering around a narrow channel or pore which is formed in the oxide, conducts ions easily, and which is opened or activated at high field strength. After building up an a localized and "bumpy" oxide layer with Ds=s_max - s_min, the channel is "closed" at sufficiently low field strength. These channels are primarily activated during the high-current phase of the oscillations whereas in both phases - open and closed channels - the oxide layer is chemically dissolved with a nearly time independent rate .

Without bothering about the required synchronization mechanism (leave alone a desynchronization mechanism) first conclusions can be drawn:

For very slow oscillations the time for building up oxide can be neglected compared to the time for dissolving oxide. The time T for one oscillation period is therefore . Using the electric field defined dynamics for the local oscillators as discussed above, we find

. (13)

For very diluted HF-electrolytes and thus small dissolution rates , we thus predict that the oscillation time increases linearly as a function of the applied voltage. This is indeed experimentally shown in [15] and gives first support for our model.

Inserting the mean oxidizing current , we eliminate the dissolution rate and find 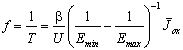. (14)

For our parameter set is comparable to J₄ in [15]. Including the absolute values of s_max - s_min=5.5 nm extracted from experimental results for Eq. (13), we find , which again is in excellent agreement with the completely independent experimental result in [15].

Finally, we are now in a position to shed some light on the "missing" sub-oxide charge detected by integrating the transient currents obtained in the high-current regime. All we have to assume is that the apparently missing interface charge escaped immediately after the voltage was turned off through the then still open channels present in this phase.

We now show that the model accounts for the increased dissolution rate required in the analysis of the transient currents. Once a channel opens, it is plausible to assume a roughly isotropic growth of silicon oxide from the tip of the channel, leading to a roughly semi-spherical oxide-"inclusion". Since the volume of the SiO₂ changes by a factor of two relative to the consumed Si, a semi-sphere of about the same size as in the bulk silicon must also occur at the electrolyte-oxide surface, leading to an increased effective oxide surface and thus to a constantly - at every cycle - replenished surface (and interface) roughness. In combination with the induced mechanical stress this may explain the experimentally observed enhanced dissolution of the "oscillating oxide" in comparison to the "static oxide" according to Eq. (1).

The model, as a new feature, contains an intrinsic synchronization mechanism; this is schematically illustrated in Fig. 5. The lateral growth of the oxide spreading from an active channel must be of the same order of magnitude as the growing oxide thickness Ds/2. This provides for a synchronization of next neighbors as can be seen from Fig. 5. If a new channel opens next to an already active one, it has to grow less oxide on one side before it turns off; it thus is "finished" earlier and in effect catching up, i.e. synchronizing itself, with the first channel.

The model, now generally speaking defined by i) an electric field induced local oscillator with highly nonlinear oxide growth caused by ionic breakthrough, ii) a coupling of next neighbor channels with a strong synchronization effect, and iii) a roughness dependent enhanced oxide dissolution, has been implemented as a Monte Carlo simulation algorithm, which, together with a number of details including a desynchronizing mechanism resulting from the decreased field strength around an active channel due to ohmic losses, will be published elsewhere. The most important results of these simulations are macroscopic current oscillations, which show all details of observed oscillations, above a critical voltage U_crit, and a non-oscillating macroscopic current below this critical voltage U_crit. The non-oscillating macroscopic current is noisy, because the local oscillators are still active, but are no longer synchronized. We thus predict that the frequency spectrum of noise measured below the critical voltage must contain a strong component at the typical frequency of the macroscopic oscillations.

The Monte Carlo simulations show an important feature of the model that is not easily predicted otherwise: the synchronization of many local oscillators proceeds by a percolation mechanism. This is demonstrated in Fig. 6, which is one example for the result of Monte Carlo simulations. Fig. 6a - c correspond to the measurements 1-3 in Fig. 1b, which is the oscillation phase of growing oxide. On the simulated area of 200 nm x 200 nm, percolative-coupled regions of about 50 nm are visible. The distribution functions of the oxide thickness as directly obtained from the simulation, are in very good agreement with those in Fig. 1b. Once again, we emphasize that the calculations and the measurements are totally independent. Fig. 6d is an example for the phase of purely chemical dissolution corresponding e. g. to measurement 7 in Fig. 1b; it shows, as required a homogeneous and narrow distribution function. It is worthwhile to point that the local oscillators are never perfectly synchronized. Even in the high-current phase of the oscillation, oxide is grown in some (percolation) regions, while in other areas only chemical etching takes place.

One more prediction shall be made: Since macroscopic current oscillations require long-range synchronization, which in turn requires percolation, and since percolation is a phenomenon of strongly nonlinear self-organizing systems, we predict that no simple differential equation will ever be found that describes all aspects of the oscillating Si-electrode.

Last, we apply the model to some particular experimental results. We first note that in interpreting experimental data it is important to keep in mind at least four different length scales: i) the channels, coupled to the current flow, occur on a sub-nm scale. ii) the local oscillators have dimensions in the nm-range. iii) an assemble of oscillators synchronized by percolation measures on the 100 nm scale. iv) the lateral resolution of the experimental setup may range from a sub-nm to the mm scale.

The capacitance, defined by the inverse oxide thickness, depends on (and thus probes) the oxide roughness on the nm-scale. AFM-measurements, as described by [4, 11], allow for lateral resolutions of about 50 nm. Ellipsometry data, as published by [5, 6, 7], measure the mean value of the oxide layer thickness in - at best - µm areas.

The broad distribution function for the oxide layer thickness, which changes strongly within one oscillation period, requires appropriate and possibly different averaging formulae for each physical parameter and concomitant experimental resolution. The integral current, e.g., depends only on the number of active channels and is thus almost independent of the mean oxide thickness. Of course, there is a coupling between the mean oxide thickness and the number of channels due to the dynamics of the locally oscillating oxide areas and the synchronization mechanism. But since this is an indirect coupling, depending on many other parameters, there is no simple relationship between the mean oxide thickness and the oscillation current.

It is easily possible, however, using the correct distribution function, to calculate the appropriate mean inverse oxide layer thickness for calculating capacitance’s. As already shown in Fig. 4b, a very good agreement between the calculated and measured capacitance of the oxide layer was obtained. It is important to point out that we neither predict nor need a significant change in the dielectric constant of the oxide layer, which has been suggested by [7]. Following the discussion above, we provide a very simple interpretation of this disagreement: The e.g., ellipsometrically measured, mean oxide thickness may not be taken as the correct value for the calculation of the capacitance . Rather, according to Eq. (12) has to be taken, which can be very different in value. What it means is that a number of parallel capacitors with different s and thus capacitance can not be replaced by one capacitor with the average thickness .

In situ AFM investigations of the "oscillating oxide" performed by [11] show an almost perfect agreement for the magnitude of the roughness in every phase of the oscillation between our data provided by the Monte Carlo situation (with parameters based on the transient current measurements), and the directly measured data by AFM. The AFM measurements provide the lateral dimension of the "roughness" as an additional parameter, something that can not be extracted from the transient currents. Areas with a diameter of about 50 to 100 nm occur and vanish again. These areas are to large to be interpreted as single local oscillations, but they fit perfectly the percolation-synchronized areas of local oscillators as shown in Fig. 6. Quantitative analysis of noise and admittance data in [14] yield the same order of magnitude of about 0.1 µm for a characteristic domain size of the oscillation. This domain size has been interpreted by the authors as the area of a local oscillator. Since we see a good correlation to the size of the percolatively coupled oscillators of our model, we believe the noise analysis relates to this parameter, but not to the local oscillators in the nm range which we introduced.

We now take a more general view of the model. Without going into details, a geometric parameter x can be defined, which determines the strength of the synchronization and therefore defines the occurrence of macroscopic oscillations; Fig. 5 shows two examples for the minimum distance d of two channels which can be active at the same moment. If this distance is large, e.g. d₁, the oxide can not grow homogeneously. If in contrast the distance d₂ is small, the oxide layer can grow nearly homogeneously because the semi-spherical oxide-"inclusions" overlap. The ratio

(15)

quantifies this parameter. The distance d is determined by the reduced electric field around a channel (the vaguely mentioned desynchronization mechanism), which in turn is given by the specific current conduction in the electrolyte above the channel. This depends, e.g., on the ion concentration, which is consequently one parameter to influence d. If x exceeds a critical value, macroscopic oscillations may occur, below x_crit only local oscillations resulting in a constant, albeit noisy are observed.

Until now we discussed only slow oscillations found at small currents and/or small HF-concentrations, with relatively thick oxide layers that are slowly dissolving, and where the oscillation current always generates oxide. For fast oscillations at larger current densities and with decreased oxide thickness, we postulate an additional current component I_no, e.g. an electronic tunneling current, which does not add to the oxidation process of the silicon. Since this current depends on the local oxide thickness, and assuming that it does not influence the oxide growth, we can calculate the overall non oxidizing current by

. (16)

D(s,U,t) is calculated as outlined before. If our model is correct, and, taking for some kind of tunneling characteristic, both the faster oscillations as well as the IU-characteristics of the silicon HF-electrolyte system can be calculated in this way by summing up the oxidizing and non oxidizing current components.

References

1. D.R. Turner: J. Electrochem. Soc., 105, 402 (1958)

2. R.L. Smith, S.D. Collins: J. Appl. Phys., 71, R1 (1992)

3. H. Föll: Appl. Phys. A, 53, 8 (1991)

4. V. Lehmann: J. Electrochem. Soc., 143, 1313 (1996)

5. J. Stumper, R. Greef, L.M. Peter: J. Electroanal Chem., 310, 445 (1991)

6. D.J. Blackwood, A. Borazio, R. Greef, L.M. Peter, J. Stumper: Electrochimica Acta, 37,

889 (1992)

7. M. Aggour, M. Giersig, H.J. Lewerenz: J. Electroanal. Chem., 383, 67 (1995)

8. J. Rappich, H. Jungblut, M. Aggour, H.J. Lewerenz: J. Electrochem. Soc, 141, L99, (1994)

9. F. Ozanam, C. da Fonseca, A. Venkateswara Rao, J.-N. Chazalviel: Applied

Spectroscopy, 51, 519 (1997)

10. H.J. Lewerenz, G. Schlichthörl: J. Electroanal. Chem., 327, 85 (1992)

11. O. Nast, S. Rauscher, H. Jungblut, H.J. Lewerenz: J. Electroanal. Chem., in press

12. H. Gerischer, M. Lübke: Ber. Bunsenges. Phys. Chem., 92, 573 (1988)

13. J.-N. Chazalviel, F. Ozanam : J. Electrochem. Soc., 139, 2501 (1992)

14. F. Ozanam, N. Blanchard, J.-N. Chazalviel: Electrochimica Acta, 38, 1627 (1993)

15. F. Ozanam, J.-N. Chazalviel, A. Radi, M. Etman: Ber. Bunsenges. Phys. Chem., 95, 98

(1991)

16. G.S. Popkirov, R.N. Schindler: Rev. Sci. Instrum., 63, 5366 (1992)

17. G.S. Popkirov, R.N. Schindler: Electrochimica Acta, 39, 2025 (1994)

18. A.E. Gershinskii, L.V. Mironova, E.I. Cherepov: phys. stat. sol. (a) 38, 369 (1976)

19. M. Matsumura, S.R. Morrison: J. Electroanal. Chem, 147, 157 (1983)

20. J. Rappich, H.J. Lewerenz: J. Electrochem. Soc, 142, 1233 (1995)

21. H.J. Lewerenz: Chem. Soc. Rev, 26, 239 (1997)

22. C. Serre, S. Barret, R. Hérino: J. Electrochem. Soc., 141, 2049 (1994)

23. S. Ottow, G. Popkirov: J. Electroanal. Chem., 429, 47 (1997)

24. J.-N. Chazalviel: Electrochimica Acta, 37, 865 (1992)

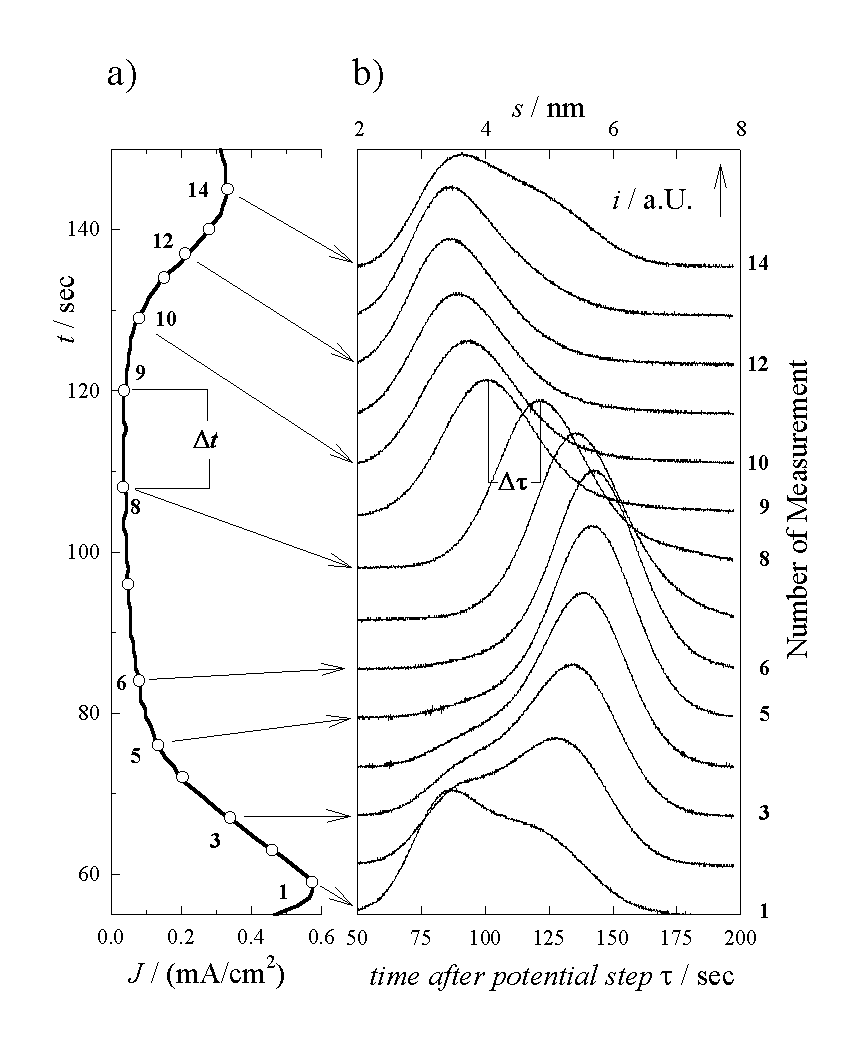
Fig. 1: a) The oscillating current density J as a function of time t applying a voltage of 4.5 V vs. SCE. Electrolyte is 0.1w% HF + 1 M NH₄Cl (volume ratio: 1:1). b) Transient currents after reducing the potential to open circuit potential at several phases of the oscillation (indicated by the arrows) as a function of time t.

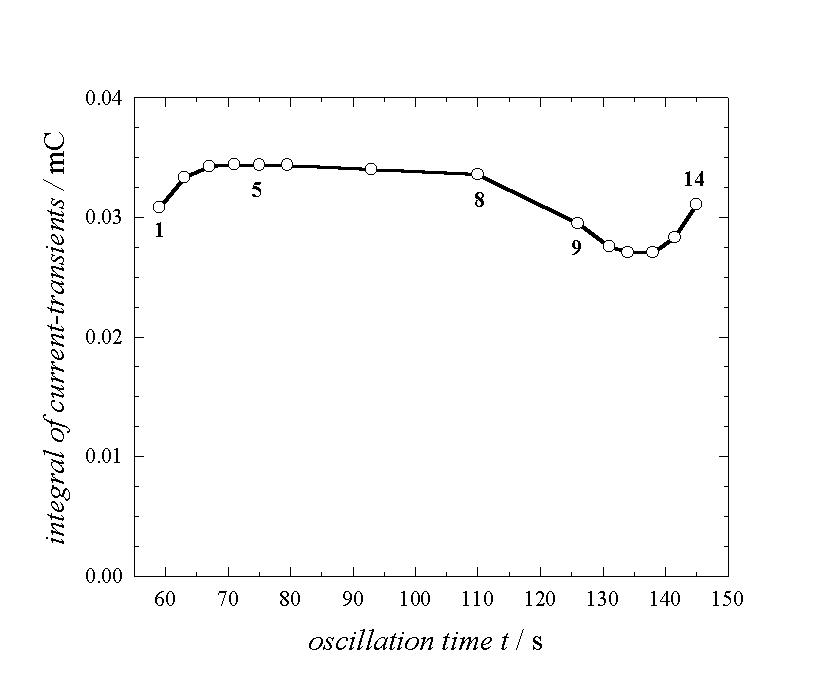
Fig. 2: Total charge released at various phases of one oscillation as obtained by integrating the current transients

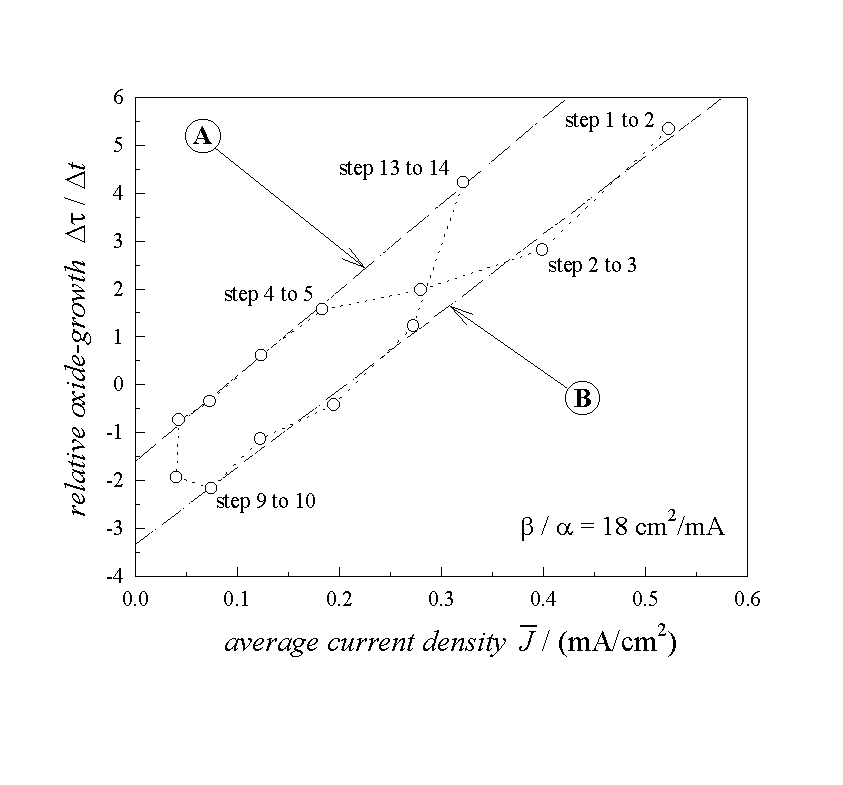
Fig. 3: Plot of the experimental results using Eq. (8). Line A and line B are calculated from a linear regression. Line A displays the correct values for the enhanced dissolution rate =1.7 and the dissolution rate a=0.04 nm / sec. Line B shows an offset, corresponding to the missing suboxide charges as outlined in Fig. 2.

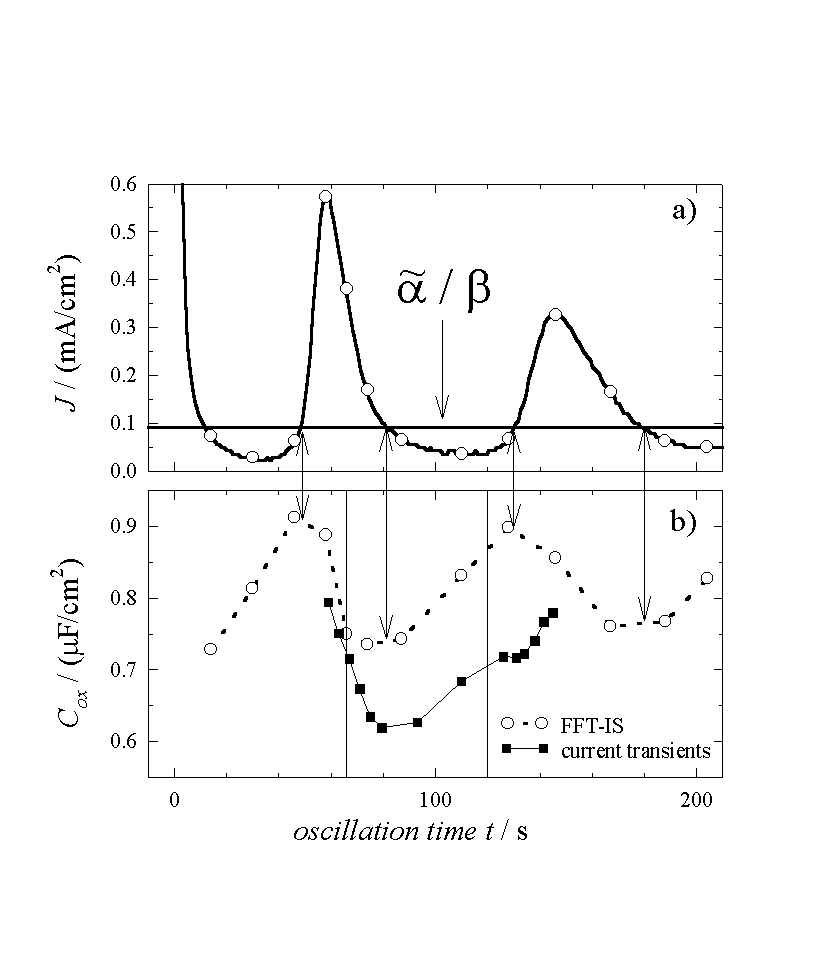
Fig. 4: a) Current oscillations (same as Fig. 1a) and the mean oxidizing current. b) Measured capacitance (dotted line) and calculated capacitance (solid line) using Eq. (12). The arrows point to the calculated maxima and minima of the capacitance.

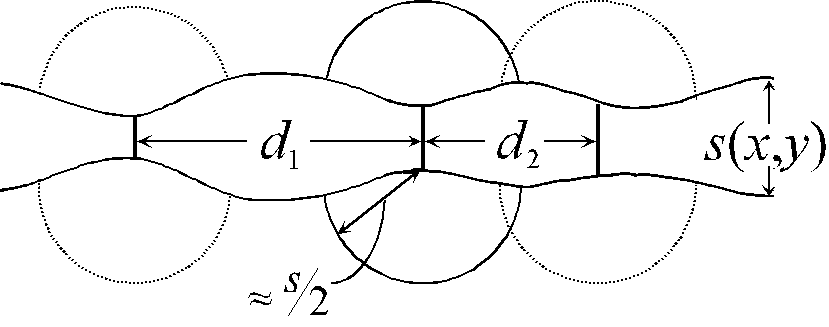
Fig. 5: The schematic cross-section through the oxide layer demonstrates some features of the oscillation model. Since the dynamics of oxide growth is defined by the electric field strength across the oxide, in a region of thin oxide (approximately s_min) an ion conducting channel opens. From the tip of the channel a roughly semi-spherical oxide inclusion is growing. The overlap between two channels is defined by the distance d between two channels and their growth radius (approximately s_max/ 2) and thus determines the coupling to neighboring areas.

Fig. 6: The maps a - d display the oxide thickness distribution of a 200 nm x 200 nm area for different phases of the oscillation as a first result of the Monte Carlo simulation. The gray colors correspond to the thickness of the oxide as lined out in the adjacent histograms. Fig. a - c correspond to the phase of growing oxide showing a qualitative agreement with the distribution function of the oxide layer thickness in measurements 1-3 in Fig. 1b. Map d demonstrates the homogeneous oxide thickness in the phase of purely chemical dissolution of oxide and can be compared with e.g. measurement 7 in Fig. 1b. The Fig. a - c exhibit a percolative growth of the oxide layer, i.e. the growing regions are coupled.