10.4.2 Was man wissen muss

	Ganz tief verinnerlicht ist der Zusammenhang von Diodenkennlinie und Solarzellenkennlinie.
		Wir verstehen, was mit den durch Licht zusätzlich generierten Ladungsträgern passiert und dass nur diejenigen, die den pn-Übergang erreichen, zum Strom beitragen. Die Bedeutung der Diffusionslänge in diesem Zusammenhang ist uns klar.
		Die wichtigen Solarzellenparameter Leerlaufspannung ("open circuit") UOC, Kurzschlussstrom ("short circuit") ISC, Füllfaktor FF, optimaler Arbeitspunkt, Wirkungsgrad h können wir erläutern und, soweit möglich, in eine Kennline eintragen
	Wir verstehen, warum bei gegebenem Sonnenspektrum der Wirkungsgrad ein Optimum für ein bestimmtes Bandgap erreicht, und wir wissen, dass mehr als h » 30 % für einen einzelnen pn-Übergang nicht möglich ist.
	Wir kennen die wichtigsten Zahlen zur Solarenergie:
		Typ. Sonnenleistung ("Europa"): 1 kW/m2 "Peak"-Solarzellenleistung: WP = 1 kW/m2 · 10 % = 100 W/m2 Mittelwert Solarleistung: Wm = WP · 10 % = 10 W/m2 Energieernte pro Jahr: Ea = Wm · 365 · 24 = 100 kWh/(a · m2) Gesamtenergiebedarf je Deutscher 6.000 kWh/a Platzbedarf für Solarzellen je Deutscher 50 m2
	Wir wissen, dass für reale Solarzellen die technische Herausforderung nur in einer Eigenschaft liegt: Sie produzieren (demnächst, so um 2015) Strom zu "grid parity"-Kosten.
		Das bedeutet 2 billige, aber gute Solarzellen / 3 Sekunden in der Fertigung – und das ist sehr schwer!
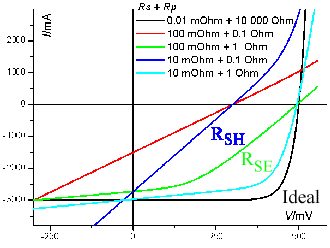
	Wir können ein Ersatzschaltbild einer realen Solarzelle geben und die Bedeutung von Shunt- und Serienwiderstand erläutern.
		Dabei ist uns klar, warum man zur Diskussion der beiden Widerstände zweckmäßigerweise die Fälle "Leerlauf" und "Kurzschluss" betrachtet.
	Wir können die wichtigsten Eigenschaften von Transistoren definieren und folgende Bilder zeichnen:
		Schematischer Aufbau Bipolartransistor. Banddiagramm Bipolartransistor. Stromflüsse im Bipolartransistor. Querschnitt MOS-Transistor
		Wir können die Stromverstärkung im Bipolartransistor erklären und in einer einfachen Näherungsformel wiedergeben, wobei wir die Näherung über die Geometrie begründen können.
		Wir können das Prinzip des MOS-Transistors beschreiben, wobei das Massenwirkungsgesetz zur Geltung kommt.
		Wir können über die Bedeutung des "O" im MOS-Transistors einiges sagen und auch Größenordnungen zur Geometrie und kritischen Größen wie Feldstärke angeben.

	Zahlen und Formeln
	Unbedingt erforderlich:
		Anmerkung: In der Regel reichen "Zehner"-Zahlen; genauere Werte sind in Klammern gegeben.
		Zahlen neu Größe   Zehnerwert Besserer Wert Technischer Wirkungsgrad Solarzellen:  »   10 % 15 % ... 20 %       Gesamtenergiebedarf und Solarzellen-Platzbedarf "Deutscher Bürger"  »   6.000 kWh/a 50 m2 Zahlen alt Größe   Zehnerwert Besserer Wert       Energielücke EG von Si = 1 eV 1,1 eV       Lebensdauer Diffusionslänge  »   Direkte HL (GaAs): ns und nm Indirekte HL (Si): ms und mm         Typische Dotierkonzentrationen in Si:  »  As od. P für n-Typ; B für p-Typ (1015 ... 1019) cm–3         Typische spezif. Widerstände r   r Metall: » 1 µWcm r Halbleiter (dotiert): » 1 Wcm r Isolator: >> 1 Wcm         Typische Energielücken EG   Metall: » 0 eV Halbleiter: » (0,5 ... 2,5) eV Isolator: > 2,5 eV         Permeabilität mr   Diamagnete: <» 1 Paramagnete: >» 1 Ferromagnete: >> 1; bis >1000         Frequenzabhängigkeit Magnetismus   relevant nur <» GHz; darüber mr » 1         Durchschlagsfestigkeiten Emax  »   (0,1 ... 10) MV/cm » 15 MeV/cm (Limit)         Maximale Stromdichten jmax   »  (103 ... 105) A/cm2           Einige Dielektrizitäts- konstanten er   e r(H2O): » 80 er(SiO2): » 3,7 er(Halbleiter): » 10 ... 20         "Interessante" Frequenzen   » 10 GHZ: Relaxation H2O » 1013 Hz: Resonanz Ionenpolarisation » 1015 Hz = "Optik": Resonanz Elektronenpolarisation         Daten Licht:    Wellenlänge    Frequenz    Energie   »     »    »   1 µm 1014 Hz 1 eV 500 nm 5 · 1014 Hz 2,5 eV         Avogadrokonstante   1024 mol–1 6 · 1023 mol–1         Bildungs- und Wanderungs- energie Leerstelle  »  1 eV ca. (0,5 ... 5) eV         (kBT)RT   »   1/40 eV = 0,025 eV         Typische Gitterkonstante a  »   1 Å = 0,1 nm 2 Å ... 5 Å         Größe eines Atoms  »  1 Å = 0,1 nm 1 Å ... 3 Å         Photonenenergie Licht  »  1 eV (1,6 ... 3,3) eV         Vibrationsfrequenz Atome im Kristall  »  1013 Hz   Formeln neu Größe Formel Stromverstärkung Bipolartransistor b  =   IK IB  =  jF(BK) jD(BE)   =  jD(EB) jD(BE)   =  NDot(E) NDot(B) Formeln alt Größe Formel Konzentration Majoritäten (Si, RT) nMaj  =  NDot     Konzentration Minoritäten (Si, RT) nMin (T)  =  ni2(T) NDot      Generationsrate, Rekombinationsrate, Gleichgewichtsbedingung R  =  G  =  nMin t   =   ni2 NDot · t     Intrinsische Ladungsträgerdichte ni  =     Neff   · exp ( –  E G 2kBT  )     Sperrstrom beim pn-Übergang = Generationsstrom jGen  =   ±e · G · L  =   ±e · L · (ni )2 NDot · t  =   const.     Diodengleichung j(U ex )  =   æ ç è e · L · (ni)2 NA · t + e · L · (ni)2 ND · t ö ÷ ø · æ ç è exp( eUex kBT ) – 1 ö ÷ ø     Ohmsches Gesetz j  =  s · E  =  E r     Spezif. Leitfähigkeit s  =  q · n · µ     "Masterformel" für Teilchendichten; hier Dichte e- im Leitungsband neL (T)   =  ¥ ó õ EL D(E) · f(E; EF,T) dE           =  Neff · exp[–(EL – EF)/(kBT)]     Dichte h+ im Valenzband n hV(T)  =  Neff · exp[–(EF – EV)/(kBT)]     Massenwirkungsgesetz ne ·nh  =  ni2     Magnetische Größen B  =   µo · H  +  J  =  µo · (H + M)  M  =   J/ µo  =  (µr – 1) · H  =  cmag   · H m r    =  cmag + 1     Dielektrische Größen m  =  q · x P  =  S m V   =  <m > · N V er    =  c + 1     Schwingungsgleichung und Resonanzfrequenz m d2 x dt2  +  mkR · dx dt  + kFx   =  q E0 cos( wt) w0 '  =  æ ç è kF m  ö ÷ ø 1/2     Komplexer Brechungsindex n (n + i k)2  =  e' – i · e''     Entropie Si Si  =   kB · ln pi     Freie Energie G G  =   U – TS     Stirling-Formel ln x!  »   x · ln x     Dichte Teilchen bei E n(E)  =  D(E) · w(E) · dE     Boltzmann-Näherung an Fermiverteilung f(E) für D E = E – EF > 2kBT f(E)   »  exp ( – D E kBT )     Boltzmannfaktor (Wahrscheinlichkeit für E) w(E)  =   exp[–E/(kBT )]     Boltzmannverteilung n(E) n(E0)  =  exp ( – E – E0 kBT )     Leerstellenkonzentration (EF : Bildungsenergie) cV  =  exp[–EF/(kB T)]     Sprungrate r atomarer Defekte (EM: Wanderungsenergie) r  =  n0 · exp[–EM /(kB T)]     Diffusionsstromdichte jDiff (Vektor!) jDiff  =  –D Ñc     Diffusionslänge L L  =  (D t)½     Coulombpotential UCou  =   e2 4p · e 0 · r     Beziehung Kraft F(r) — Potential U(r) F(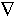r)  =   – U(r)     Mech. Spannung s, Dehnung e, E-Modul E s  =  F A e   =   l(s)  –  l0 l0 E   =   ds de     Innere Energie pro Freiheitsgrad (Gleichverteilungssatz; einzelnes Teilchen) UFreiheitsgrad  =  ½kBT     Mittlere thermische Energie eines klassischen Teilchens (innere Energie; Def. der Temperatur) UTeilchen  =   ½fkB T (f: Anzahl der Freiheitsgrade)     Thermische Energie (Größenordnung von UTeilchen) Etherm  =  kBT (UTeilchen  »  kBT)

© H. Föll (MaWi für ET&IT - Script)