|
Kontakte oder "junctions" machen Bauelemente. |
|
|
 |
Es gibt kein Halbleiterbauelement ohne Halbleiter-Metall
Kontakt und so gut wie keines ohne "pn-Kontakt". |
|
 |
Kontakte bei Halbleiterbauelementen macht man nicht durch "kontaktieren" im Sinne
von "Zusammendrücken" sondern durch (extrem trickreiche) Halbleitertechnologie. |
|
 |
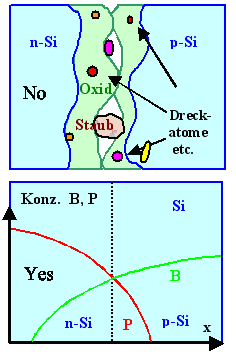
Ein pn-Übergang liegt vor an der Stelle, an der die Akzeptor- und Donatorkonzentration
gleich groß ist. |
|
 |
"Ohmsche Kontakte", die man immer braucht, sind
idealerweise eigenschaftslos, d. h. sie lassen bei jeder Spannung und Polarität den vollen Strom durch. Sie sind aber
oft recht schwer zu machen. |
| |
| |
 |
Links und rechts von einem Übergang können vor Kontakt unterschiedliche
Fermienergien vorliegen. |
|
|
 |
Þ
Es gibt unterschiedliche Ladungsträgerkonzentrationen. |
|
 |
Þ Es gibt unterschiedliche Zustände in der Energielücke
bei "homo"-Kontakten wie dem pn-Übergang im Si. |
|
 |
Beispiel: "Kontakt" Simit der Oberfläche
des Si-Kristalls. |
 |
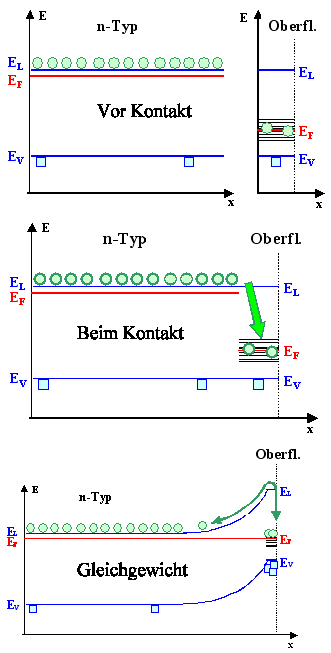
Es ist extrem wichtig, das Bild Þzu
verrstehen! |
|
 |
Vor Kontakt: "Irgendwie" verschiedene Si-Varianten = verschiedene
Zustände in der Energielücke = verschiedene Fermienergien. |
|
 |
In der (Pico)sekunde nach (gedachtem) Kontakt fließen Elektronen auf jetzt verfügbare
Zustände mit niedrigerer Energie (im Beispiel nach rechts zu den Oberflächenzuständen); Löcher laufen
auf neu verfügbare (mit Elektronen besetzte) Plätze mit höherer Energie. |
|
 |
In der Nähe des Kontakts herrscht keine Ladungsneutralitität mehr. Im Beispiel lädt
die Oberfläche sich negativ auf durch den Zustrom von Elektronen, die jetzt aber auf
der Oberfläche lokalisiert sind. |
|
 |
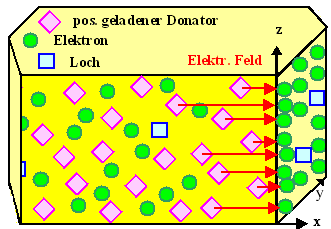
Im Volumen nahe der Oberfläche bleiben díe ortsfesten positiv geladenen Donatoratome
zurück; sie bilden eine Raumladung
mit der Dichte N+Don. |
|
 |
Dadurch entsteht ein elektrisches Feld, das die zur Oberfläche
strebenden Elektronen zurücktreibt. |
|
 |
Die rechte Seite des Banddiagramms geht deshalb energetisch "hoch", es entsteht
eine Bandverbiegung. |
| |
| | |
 |
Entscheidend ist das Banddiagramm für Gleichgewicht.
Einige Definitionen dazu, die alle im Grunde dasselbe sagen: |
Ü Vollständig äquivalente
Formulierungen
Damit Rezept für Banddiagramm-Erstellung: |
| 1. |
Zeichne die Fermienenergie als horizontale Linie;
markiere den Übergang. |
| 2. |
Zeichne "weit" links davon das Banddiagramm von Material 1; weit rechts das von Material 2;
immer relativ zu der bereits festgelegten Fermienergie. | | 3. |
Verbinde Leitungs- und Valenzband
durch eine "gefühlsmäßig" gezeichnete Bandverbiegung.
|
|
|
 |
Gleichgewichtliegt vor, sobald es genausoviel Energie kostet gegen das Feld anzulaufen,
wie man durch "Tieferfallen" an der Oberfläche gewinnen kann. |
|
 |
Gleichgewicht liegt vor, sobald energetisch nichts mehr zu gewinnen ist. Þ
Die Fermienergie ist überall dieselbe. |
|
 |
Gleichgewicht liegt vor, sobald der nach rechts fließende Elektronenstrom
genau so groß ist wie der zurückfließende Strom. |
|
 |
Ströme fließen, weil es für Elektronen auf beiden Seiten eine Wahrscheinlichkeit
exp(–DE/kT) gibt, die Energiebarriere
DE zur jeweils anderen Seite zu überwinden. |
| | |
| |
 |
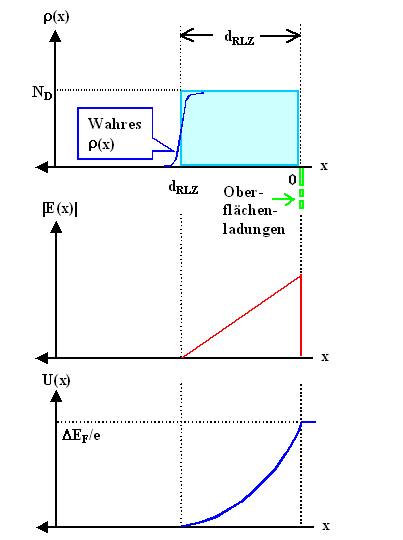
Eine Darstellung im Ortsraum verdeutlicht
das Konzept der Raumladungszone. |
|
|
 |
Es gibt "Ladungen im Raum", da die ionisierten Dotieratome nicht beweglich sind
und "ihre" Ladungsgträger jetzt woanders sind. |
|
 |
Das elektrische Feld beginnt und endet auf den jetzt separierten
Ladungen. |
|
 |
Wir haben unvermeidlich einen geladenen Kondensator
mit der Kapazität CRLZ. |
| | |
|
| | |
| |
 |
Formal-mathematisch wird die Poisson-Gleichung
gelöst (Grundgleichung der Elektrostatik). |
|
|
 |
Die Poisson-Gleichung beschreibt den Zusammenhang zwischen Ladungsdichte r , elektr. Feld E und elektr. Potential V. |
| | |
|
|
|
| DV(x, y, z) | = –
| r
ee0 | |
| | | |
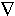 V(x, y, z) V(x, y, z) | = |
– E(x, y, z) |
|
|
| | |
|
 |
Lösungsweg eindimensional: |
|
 |
Ladungsdichte
r = NDot in dRLZ = const. |
|
 |
Feld
E = einmal integrieren = Gerade. Randbedingung: E(x = dSCR) = 0
V/cm |
|
 |
Potential
V = zweimal integrieren = Parabel. Randbedingung V(dSCR) = 0
eV; Potentialdifferenz = DEF/e |
© H. Föll (MaWi für ET&IT - Script)