|
Dichte der Elektronen im Leitungsband: |
|
| nL(T) = |
¥
ó
õ
EL |
D(E) · f(E, T) · dE |
= | 4.8 · 1015 · T
3/2 · exp – | EL – EF
kT | cm– 3 |
|
|
|
 |
Erster Teil der Formel gilt immer |
|
|
 |
Zweiter Teil der Formel enthält div. Näherungen |
|
 |
Dichte der Löcher im Valenzband |
| |
|
 |
Löcher verhalten sich wie positiv geladene Elektronen |
|
| nhV(T) = |
¥
ó
õ
EL |
D(E) · [1 – f(E, T) ] · dE |
= | 4.8 · 1015 · T
3/2 · exp – | EF – EV
kT | cm– 3 |
|
|
|
 |
Löcher haben eine positive Elementarladung, tragen Strom, haben eine Masse und eine Beweglichkeit. |
|
| |
| |
| |
 |
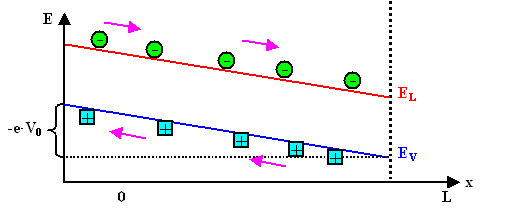
Ein elektrisches Feld "verbiegt" die Bänder um die jeweilige elektrostatische
Energie, d.h. um e · V, V = elektrostatisches Potential. |
|
|
|
 |
Die lokale Bandverbiegung zeigt die Richtung des induzierten Teilchenflusses: Elektronen "abwärts",
Löcher "aufwärts". | |
|
 |
Bei Stromfluß herrscht Nichtgleichgewicht; damit gibt es streng genommen keine Fermienergie
mehr. | |
| |
| |
|
 |
Dotieren: gezieltes Einbringen von Defekten,
die in der Bandlücken Zustände für Elektronen nahe den Bandkanten erzeugen. |
|
| nL | = |
¥
ó
õ
EL |
D(E) · f(E, EF
,T) · dE |
» NLeff . exp – |
EL – EF
kT | | |
| | |
| | | nV
| = | EV
ó
õ
–¥ |
D(E) · [1 – f(ED, EF,
T)] · dE |
» NVeff . exp – |
EF – EV
kT |
|
|
|
 |
Donatoren: leichte Elektronenabgabe ins Leitungsband
(P und As für Si) | |
|
 |
Akzeptoren: leichte Elektronenaufnahme (= Löcherabgabe
ans) aus dem Valenzband (B in Si) | |
 |
Ladungsträgerdichten aus "Master"formel; aber jetzt mit Zuständen
im Bandgap (Zustandsdichte = Dotierstoffdichte bei E-Niveau des Dotierstoffs) und verschobener Fermienergie |
|
|
| |
| |
 |
Fermienergie aus Ladungsneutralität. |
|
| Art | Formel | Graphik |
| Elektronen in L |
nL = NeffL · f(EL
, EF , T) |
 | | negativ ionisierte Akzeptoren |
N+A = NA · f(EA
, EF , T) |
| Löcher in V |
nV = NeffV · {1 – f(EV
, EF , T)} |
| positiv ionisierte Donatoren |
N–D = ND · {1 – f(ED
, EF , T)} |
|
|
 |
Resultierede transzendente Gleichung nicht analytisch lösbar. |
|
 |
Näherungen sind einfach und ergeben: |
|
|
 |
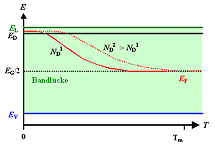
EF ungfähr beim Dotierstoffniveau für kleine und mittlere Temperaturen. |
|
|
 |
EF wandert mit zunehmender Temperatur in Richtung Bandmitte. |
|
|
| |
| |
 |
Mit Dotierung werden Majoritäten und
Minoritäten erzeugt, die Halbleiter werden n- oder p-leitend. |
|
| nL · nV |
= | ni2 |
| nmin | = |
ni2
NDot |
|
|
|
 |
Es gilt immer das Massenwirkungsgesetz; Kenntnis einer
Konzentration ermöglicht Berechnung der jeweils anderen. |
|
|
 |
Bei mitttleren Temperaturen ( » RT bei Si)
ist die Majoritätskonzentration in etwa gleich der Dotierstoffkonzentration; damit ergeben sich besonders einfache
Verhältnisse. | |
| | |
| |
 |
Beweglichkeit µ: Wird durch Dotierung reduziert. |
|
|
 |
Spez. Leitfähigkeit bzw. Widerstand: Im wesentlichen durch Dotierstoffkonzentration
bestimmt. | |
|
| |
|
 |
Generation und Rekombination zwischen den Bändern: Bei Minoritäten sehr
viel stärker "fühlbar" als bei Majoritäten |
|
|
|
 |
Nach wie vor Gleichheit der Raten im Gleichgewicht. |
|
|
 |
Lebensdauer t (der Minoritäten) und Diffusionslänge
L weiterhin direkt gekoppelt. | |
 |
Zwischen Beweglichkeit und Diffusionskonstante D existiert immer
die einfache Einstein-Smoluchowski Beziehung |
|
|
| |
|
| |
|
| | |
| |
© H. Föll (MaWi 2 Skript)