|
Auch die Elektronen(wellen) des Kristall werden gebeugt; es gilt die Bragg-Bedingung: |
|
|
 |
Die Bragg-Bedingung ist für alle Zustände (= kB;
nicht mit Boltzmannkonstant kB verwechseln!) erfüllt, die auf
den Rändern einer Brillouinzone liegen |
|
 |
Brillouinzonen sind die ineinandergeschachtelten Polyeder im reziproken Gitter, die man mit
der "Mittelhalbierenden" Konstruktion erhält. |
|
 |
Die 1. BZ ist die Wigner-Seitz EZ des reziproken
Gitters. |
| |
| |
 |
Die Untermenge der gebeugten Elektronenwellen überlagern sich zu stehenden
Wellen; es gibt grundsätzlich zwei Möglichkeiten: |
| y± = exp(ikBr) ± exp(–ikBr) | |
| y+max = |
n · a | |
| n = 0, 1, 2, 3,... |
| | | |
| |
| y–max = |
n · a + a/2 |
| n = 0, 1, 2, 3,... |
|
|
|
 |
Die Maxima der stehende Wellen liegen bei oder zwischen
den Gitterpunkten/Atomen (a = Gitterkonstante). |
|
 |
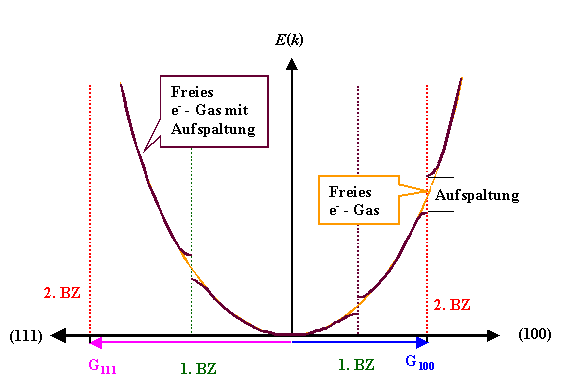
Die zugehörigen Energien müssen verschieden
sein; wir erhalten auf den Rändern der Brillouinzonen eine Energieaufspaltung der E(k)-Parabel. |
| |
| |
 |
Das kann nur so aussehen: |
|
|
 |
Nur in der Nähe einer BZ ist die freie Elektronengas Dispersionskurve "verbogen";
direkt auf der BZ macht sie einen Sprung, d.h. erlaubt zwei Energiewerte für
ein k. |
|
 |
Qualitativ bleibt in dieser Betrachtung nur die Größe der Aufspaltung und der Verlauf
in der Nähe der BZ. |
 |
Reale Dispersionskurven können auch zwischen
BZ von der idealen "freien Elektronengasparabel" abweichen |
|
|
|
 |
Insbesondere müssen die Maxima und Minima nicht
immer auf der BZ liegen. | |
|
 |
Die Größe der Energieaufspaltung ist ein Materialparameter |
|
|
| |
| |
 |
Ein Banddiagramm ist die stark vereinfachte Pauschaldarstellung der erlaubten
Energien. | |
|
|
 |
Nur Valenzband (letztes mit Elektronen teil- oder vollbesetztes
Band) und das darüberliegende Leitungsband sind wichtig |
|
|
 |
Ein Band hat genau so viele Zustände wie die Zahl der EZ im Kristall |
|
|
 |
Die Bandstruktur ist ein "Materialparameter"; wichtig ist die Größe der
Energielücke EG. | |
| | |
|
 |
Allein die Größe der Energielücke entscheidet darüber, ob
ein (perfekter) Kristall ein Leiter (= Metall; Halbmetall), Halbleiter oder Isolator ist. |
|
|
| |
| |
 |
Bei Band-Band Übergängen gelten Energie- und (Kristall)impulserhaltungssatz |
|
e–(V) + E Þ e–(L)
+ h+(V)
E ³ EG |
k – k' =
G
|k| ¹ |k'|
G = reziproker Gittervektor |
|
|
 |
Energiezufuhr: Thermisch oder Photonen;
Energieabgabe: Thermisch oder Photonen |
|
|
 |
Kristallimpulserhaltungssatz: Auf inelastische Stöße verallgemeinerte Braggbedingung.
Verhindert Großteil der energetisch erlaubten Übergänge. |
|
|
| |
| |
 |
Reduzierte Banddarstellung: Zeichentechnischer "Trick" erlaubt einfachste
Darstellung der möglichen Übergänge. | |
|
|
 |
Nur Übergänge senkrecht nach oben (= Generation) oder nach unten (= Rekombination)
sind erlaubt. | |
|
| |
| |
 |
Direkte und indirekte Halbleiter: Rekombination (nach Thermalisierung) einfach
beziehungsweise "unmöglich" (= schwer). | |
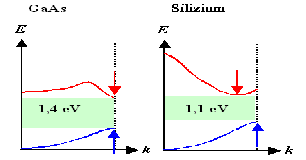 | Direkte Halbleiter:
Lichtemission bei Rekombination
IndirekteHalbleiter:
Strahlungslose Rekombiation
(über Defekte) |
|
|
 |
Direkte Halbleiter (GaAs, GaAlAs, InP, GaN, ...) sind Materialien
der Optoelektronik/Photonik. | |
|
 |
Direkte Halbleiter (Si, Ge, ..) sind Materialien der Mikroelektronik |
|
|
| |
| |
 |
Lebensdauer
t: Zeit zwischen Generation und Rekombination. |
|
Direkte Halbleiter: t; L klein: ns bzw nm.
Indirekte Halbleiter: t; L groß; stark defektabhängig; bis zu s
bzw. mm. |
|
|
 |
Diffusionlänge L = (Dt)½: Im
Mittel zurückgelegte Strecke | |
|
 |
t und L sind sehr wichtige Materialparameter. |
|
|
| |
| |
| | |
|
| | |
| |
|
© H. Föll (MaWi 2 Skript)