1.1.2 Elektrische Leitfähigkeit
Diejenige elektronische Eigenschaft von Materialien, die einem als erste einfällt, ist die elektrische Leitfähigkeit.
Bei der elektrischen Leitung ist der Zusammenhang zwischen Strom und Spannung durch das Ohmsche Gesetz gegeben:
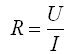 | (1.1) | |
R: Widerstand [R] = W U: Spannung [U] = V I: elektrischer Strom [I] = A
Bei dieser Schreibweise des Ohmschen Gesetzes ist man auf die Betrachtung eines speziellen Falles beschränkt. Es gilt nur für den betrachteten Leiter mit dem Widerstand R.
In der Materialwissenschaft ist man jedoch mehr an einer Beschreibung von allgemeinen Grundeigenschaften von Werkstoffen interessiert. Weiterhin möchte man das Verhalten von Werkstoffen durch die zu Grunde liegenden physikalischen Gesetzmäßigkeiten erklären.
Man verwendet daher häufig eine allgemeinere Schreibweise des Ohmschen Gesetzes. Anstelle des elektrischen Stromes geht man zur Stromdichte über, die auf den Leiterquerschnitt F normiert ist und damit unabhängig von einem speziellen Querschnitt:
Die Einheit der elektrischen Stromdichte ist also [j] = A/m2
Unter der Berücksichtigung des elektrischen Stromes I
läßt sich die Stromdichte auch schreiben als
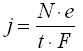 | (1.2) | |
Dabei sind
q = Ladung des Teilchens, i.d.R. ist das gleich der Elementarladung e: e = 1.602· 10-19 As N: Zahl der Ladungsträger
Weiterhin kann man die Spannung U durch die elektrische Feldstärke E ausdrücken (vorausgesetzt wird ein homogenes Feld):
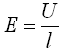 | (1.3) | |
l: Länge des Leiters.
Mit diesen Definitionen läßt sich das Ohmsche Gesetz (1.1) jetzt schreiben als
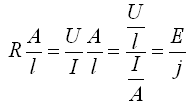 |
Schließlich wird die Größe
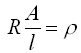 | (1.4) | |
als spezifischer Widerstand definiert, eine Größe, die jetzt unabhängig von speziellen Materialgrößen ist und für einzelne Materialklassen definiert, z.B. für alle Kupferleiter mit einer bestimmten Verunreinigungskonzentration. Es gilt der Zusammenhang
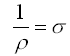 | (1.5) | |
mit s, der elektrischen Leitfähigkeit. Die Einheit der elektrischen Leitfähigkeit ist[s] = W-1m-1.
Das allgemeinere Ohmsche Gesetz lautet damit an Stelle von (1.1)
| j = s · E | (1.6) | |
Bei der Stromdichte handelt es sich genauer betrachtet um einen Vektor, der in Richtung parallel zur Richtung der Driftgeschwindigkeit vD der Ladungsträger verläuft (vergleiche Abbildung 1.1)
Die Driftgeschwindigkeit ergibt sich aus der mittleren Geschwindigkeit aller Elektronen eines elektrischen Stromes. Sie ist sehr klein, im Gegensatz zu den Geschwindigkeiten einzelner Elektronen, da zu der überwiegenden Anzahl der Geschwindigkeisvektoren einzelner Elektronen ein Geschwindigkeitsvektor gleicher Größe, aber entgegengesetzter Richtung existiert. Im Mittel bleibt daher nur eine geringe „Nettogeschwindigkeit“ der Elektronen, die Driftgeschwindigkeit, übrig.
 |
| Abb. 1.1: Elektronengas, welches sich mit der Driftgeschwindigkeit vD durch den Querschnitt A bewegt. Die Einzelgeschwindigkeiten einiger Elektronen sind angedeutet. Mit Hilfe des unteren Teils ist schematisch gezeigt, wie aus sehr vielen einzelnen Elektronengeschwindigkeiten die DriftgeschwindigkeitvD entsteht. |
Auf Grund der oben gegebenen Definition der Stromdichte leitet man her:
| (1.7) | ||
Dabei ist
ne: Elektronendichte = (Zahl der Elektronen)/Volumeneinheit [ne] = m-3
Die Länge l ist die Strecke, die die Elektronen im Mittel in der Zeit t zurücklegen.
In vektorieller Schreibweise lautet das Ohmsche Gesetz
| j = s· E | (1.8) | |
Gleichung (1.8) berücksichtigt eine mögliche Anisotropie des elektrischen Leiters. Nicht in jedem Fall muß j parallel zu E sein (z.B. nicht für nicht-kubische Kristallgitter). Die in Gleichung (1.8) zwischen den beiden Vektoren j und E vermittelnde Größe s ist im Prinzip ein Tensor (Leitfähigkeit-Matrix).
Damit wird die Fähigkeit eines Ladungsträgers beschrieben, auf ein elektrisches Feld zu reagieren. Je größer die Beweglichkeit, desto größer ist die Driftgeschwindigkeit des Ladungsträgers unter dem Einfluß des elektrischen Feldes:
| vD = m· E | (1.9) | |
[m] = (m/s) / (V/m) = m2/ (Vs)
Für das Ohmsche Gesetz (Gl. (1.8)) kann man dann schreiben
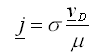 |
Ein Vergleich mit Gleichung (1.7) liefert den Zusammenhang
| s = ne · e · m | (1.10) | |
d.h. die elektrische Leitfähigkeit ist um so größer, je höher die Beweglichkeit und je größer die Elektronendichte ist.
Die elektrische Leitfähigkeit für ein gegebenes Material wird unter anderem beeinflußt durch Gitterdefekte, wie Versetzungen und Verunreinigungen (vergleiche Teil I der Vorlesung).
| Werkstoff |
s [W-1 cm-1] |
| Supraleiter (T < TC) |
oo |
| Silber |
67.1·106 |
| Kupfer |
64.5·106 |
|
Si (undotiert) | 4.3·10-6 |
| Quarz | 10-10 |
| Vakuum | 0 |
| Tabelle 1.1: Typische Leitfähigkeiten von Leitern, Halbleitern und Isolatoren bei Raumtemperatur. | |