 |
Kann man für vernüftige Dicken d ein
1 m langes Schwert produzieren, das sich rein elastisch in einen Halbkreis biegen läßt? |
|
Das geht nur, wenn die Dehnung des am stärksten gedehnte Teils noch im elastischen
Bereich liegt. |
|
 |
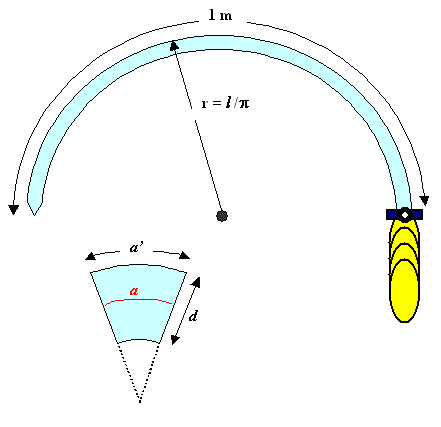
Am stärksten gedehnt ist der kreisäußere Teil des Schwerts. In
Aufsicht sieht das so aus: |
| |
|
|
In dem (übertrieben dick dargestellten) Segment wird klar, daß die
Außenseite gedehnt, und die Innenseite gestaucht ist. Genau in der Mitte läuft die gedachte (rot
gezeichnete) "neutrale Faser", die nicht verformt ist, d.h. sie ist immer noch 1 m lang |
|
|
Die Dehnung e der Außenseite in dem gezeichneten
Segment ist (a' – a)/a; sie ist entlang des Schwertes in jedem Segment überall gleich
groß solange wir einen Halbkreis haben. |
|
|
Elementare Geometrie ergibt für ein in einen Halbkreis gebogenes Schwert
der Länge l und der Dicke d |
|
|
|
|
Die Verformung bleibt elastisch, solange in der am stärksten verformten Außenseite
nicht die Fließspannung RP erreicht wird, ab der sich das Material plastisch verformen würde.
(Wir ignorieren dabei, was bei Stauchung so alles passieren könnte). |
|
|
Die Spannung ist bei elastischer Verformung mit der Dehnung über den E-Modul
verknüpft. Damit wird die Verformung elastisch bleiben, solange gilt |
| |
| s | = |
E · e < RP |
| | | | |
p · d · E
2 l |
< | RP |
| | | | | d |
< | 2 RP · l
p · E | |
|
|
|
Mit den Zahlenwerten E = 100 GPa, RP = (0.5
- 2) GPa, l = 1 m erhält man sofort |
|
|
| d | < |
2 · 0.5 · 1
3.14 · 100 |
N · m · m2
m2 · N |
= | 3.18 mm | | |
| | |
2 · 1
3.14 · 100 |
N · m · m2
m2 · N |
= | 12,74 mm |
|
|
|
Die Antwort lautet also: Ja es geht - im Prinzip. Denn vorausgesetzt haben wir,
dass das Schwert vollständig homogen ist, d. h. keine lokalen Schwachstellen hat, und dass es die Dehnung, nicht die
Stauchung ( = negative Dehnung) ist, die die plastische Verformung oder dne Bruch bestimmt. |
| |
© H. Föll (MaWi 1 Skript)
Mit Frame
Übung 7.1-3 Schwertbiegen