Spannungszustände und Konsequenzen für eine allgemeine Ebene

	Im Hauptteil haben wir die Spannungen in einer beliebig orientierten Ebene berechnet, wobei sich das beliebig aber nur auf den einen Winkel relativ zu einer der beiden möglichen, senkrecht zur Zugrichtung stehenden Achsen bezog.
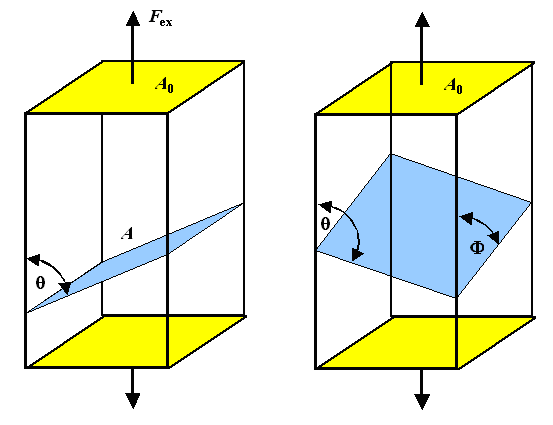
		Die Situation ist im Bild links noch einmal dargestellt, der Winkel q beschreibt die Geometrie vollständig.
	Rechts ist der jetzt wirklich allgemeinste Fall einer beliebig orientierten Ebene. Wir brauchen einen zweiten Winkel F um die Lage der Ebene zu charakterisieren.
		Wie groß ist jetzt die Normal- und Scherspannung in dieser Ebene?
		Das ist immer noch ziemlich elementare Geometrie; die wir im Detail weder nachvollziehen müssen noch wollen. Das Ergebnis ist nämlich nicht sonderlich interessant.
	Interessant ist nämlich nur die in der betrachteten Ebene in Richtung der Gleitrichtung wirkende Schubspannung.
		Die Gleitrichtung ist die Richtung in der die Ebenen aufeinder abgleiten (wie vielleicht am klarsten in einem Bild in Kap. 8 dargestellt). Letztlich interessiert nur die Spannung in dieser Richtung.
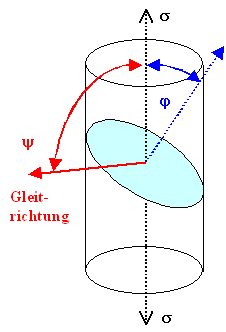
		Die gesuchte Formel wird am einfachsten, wenn man die beiden die Ebene charakterisierende Winkel anders definiert. Wir nehmen, wie nebenstehend dargestellt: j = Winkel zwischen Ebenennormale und Zugrichtung y = Winkel zwischen Zugrichtung und Gleitrichtung
		Das beschert uns die extrem simple Formel für die Schubspannung t in Gleitrichtung
		t  =  s · cosj · cos y
		Diese Gleichung ist auch als Schmidsches Schubspannungsgesetz bekannt, cosj · cos y ist der Schmidfaktor des betrachteten Gleitsystems.
	Simpel, aber nicht ganz ohne. Was ist der maximale Schmidfaktor eines gegeben Kristalls? Mache ich j = 0, habe ich zwar den größtmöglichen cosj; aber gleichzeitig wird unweigerlich cos y = 0.
		Letztlich wird man bei j = 450 landen, wie gehabt, und eine Gleitrichtung in der großen Achse der Ellipse im nebenstehenden Bild.
		Wie auch immer: Sobald die mit dem Schmidfaktor brechnete Schubspannung auf irgendeiner Gleitebene in einer der möglichen Gleitrichtungen den kritischen Wert erreicht, beginnt Versetzungsbewegung und damit plastische Verformung.

Mit Frame

8.2.1 Beobachtungen und Interpretation

7.1.2 Normal- und Scherspannungen

© H. Föll (MaWi 1 Skript)