 |
Ein richtiger Kristall ist immer streng periodisch. Ein Baustein - die Basis
- wiederholt sich in strenger Sequenz; es ist nicht unähnlich wie der Bau einer (dicken) Mauer mit Ziegelsteinen, die immer dieselbe Form haben.
|
|
 |
Man kann auch zwei oder mehr verschiedene Ziegelsteine
haben (zweidimensional wären es Fliesen); die Aufgabe ist immer,
den Raum oder die Fläche komplett zu füllen, und das geht nur - so dachte
man - in streng periodischen Arrangements. |
 |
Bis dann 1984 am National Institute of Standards and Technology in Gaithersburg, Md.,
USA, der Gastforscher Dan Shechtman vom Israel Institute of
Technology in Haifa zu seiner Verblüffung fand, daß eine Al - Mn Legierung, die er eigentlich als kristallin
kannte, die konventionellen Regeln der Kristallographie nicht befolgte - aber trotzdem
definitiv nicht amorph war.
Geglaubt hat man es ihm zunächst nicht; er wurde lange und heftig angefeindet. 2011
hat er dann aber (endlich) den Nobelpreis für Chemie (!) bekommen. Dieser
Link führt zu ein paar lesenwerten Details der MRS (Materials Research Society). |
|  |
Im Rasterelektronenmikroskop waren geometrische Körper mit glatten Oberflächen zu sehen - typisch
für Kristalle - aber sie hatten eine fünfzählige Symmetrie!
|
|
 |
Vom normalen kristallinem Aufbau verschieden war, daß der Abstand von (für sich
kristallinen) Atomreihen nicht fest war (wie für einen richtigen Kristall), sondern unsystematisch zwischen zwei festen
Werten variierte. Zweidimensional kann man sich das etwa so vorstellen wie nachfolgend gezeichnet |
| |
 |
| Courtesy Dr. P. Steinhardt, Princeton University |
|
 |
Diese Muster mit typischen fünfzähligen "Sternen" kann man bekommen, wenn
man die links dargestellen Fliesen immer nur so kombiniert, daß keine Brüche in den Linien auftreten. |
|
 |
Das sich dann ergebende Farbmuster ist auch ziemlich beeindruckend. Insbesonders sieht man
sofort die vielen schönen Fünfecke, die eine fünfzählige Symmetrie
vortäuschen, die aber gar nicht da ist. |
|
 |
Der reinen Mathematik war das nicht so neu. Sie hatte schon viel früher die Frage beantwortet,
ob die Ebene mit einer endlichen Anzahl von verschieden geformten Fliesen einerseits
vollständig bedeckt werden konnte, andererseits in nichtperiodischer
Weise. |
|
 |
Die Antwort war stark davon abhängig, wie die Frage gestellt war. Suchte man 1.
Fliesen, die sowohl periodisch als auch nichtperiodisch
eine Fläche vollständig bedecken konnten, oder
2. Fliesen, die nur nichtperiodische Muster erlaubten? |
|  |
Zur ersten Frage gibt es viele Lösungen, die eleganteste
ist die "versatile Fliese" (versatil = wendig, beweglich,
vielseitig), sie heißt auf auf Englisch passend "Versatile"
(tile = Fliese). |
|
 |
Die zweite Frage führt ziemlich schnell in die tiefsten Abgründe
der Mathematik. |
 |
Die dreidimensionalen real beobachteten Quasikristalle
kann man sich nun immer entlang den folgenden zweidimensionalen Analogien aufgebaut denken - auch wenn's schwer fällt. |
|
 |
Die nachfolgenden Bilder zeigen periodische und aperiodische Strukturen, die beide mit der
"Versatile"möglich sind. Sie sind Illustrationen aus dem Buch "The
Emperors new Mind" von Roger
Penrose nachempfunden; dort finden sich mehrere vollständige und schönere Bilder. Die "versatile
Fliese", die "Versatile" ist dabei das einzelne sichelförmig gebogene Dreieck wie dargestellt |
|
 |
Mit der Versatile läßt sich zunächst ein
simpler Kristall darstellen: |
| |
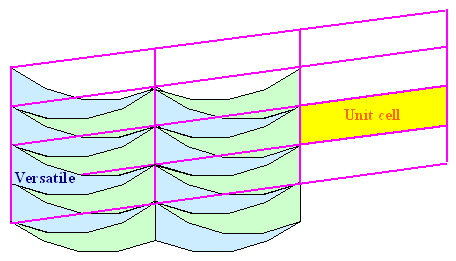 |
| Möglicher zweidimensionaler Kristall
mit der Versatile. |
|
|
 |
Mit Variationen und Fortsetzungen der hier gezeigten Anordnung lassen sich aber auch mehrere
Arten von Spiralen darstellen, die den "Boden" lückenlos bedecken, aber ganz sicher keine Translationssymmetrie
haben. |
| |
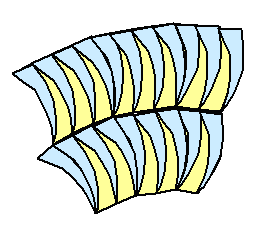 |
Kann bei Fortsetzung nicht kristallin werden (ist aber
auch nicht typisch amorph)
sondern produziert bei geeigneter Fortsetzung aperiodischen
spiralige Muster. |
|
 |
Will man nur Fliesen zulassen, die ausschließlich
nichtperiodische Muster ergeben, wird die Lösung komplizierter. |
|
 |
Berger konnte 1966 zeigen,
daß es zwar einen Satz Fliesen gab, der nur nichtperiodische Muster erzeugte,
aber dieser (mathematische) Fliesensatz hatte 20 426 verschieden Fliesen. Er wurde zwar schnell auf "nur"
104 reduziert, aber praktische Bedeutung hatte das nicht. |
 |
Dann kam 1974 Roger Penrose von der Universität Oxford und zeigte, daß man mit zwei
Fliesen auskommen kann - einem dicken und einem dünnen Rhombus. |
|
 |
Mit den beiden ""Penrose Fliesen""
kann man jede Ebene nur nichtperiodisch bedecken
falls man sich an bestimmte Regeln hält, die z.B. durch die Farbe der Fliesenränder vorgegeben sind (sonst wird's
periodisch). |
|
 |
Das sieht dann so aus wie unten gezeigt. Das rotumrandete "Fliesencluster" unten
rechts zeigt eine häufig auftretende Überstruktur. Im Zentrum des Bildes ist gezeigt, wie sich der zweidimensionale
Quasikristall auch durch häufiges Überlappen der hervorgehobenen Überstruktur darstellen läßt. |
| |
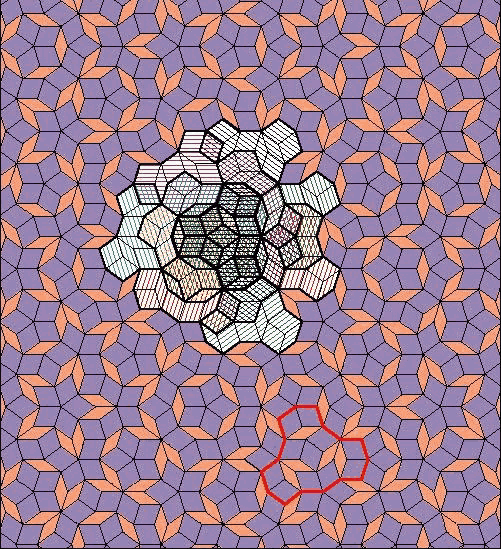 |
| Courtesy Dr. P. Steinhardt, Princeton University |
|
|
Die "Penrose tiles" sind nicht nur für die
Materialwissenschaft der Quasikristalle wichtig, sie können auch sehr schön einen fundamentalen mathematischen
Satz demonstrieren (der von Penrose immer wieder bemüht wird, um das menschliche
Bewußtsein unter die natürlichen Phänomene zu subsummieren): |
|  |
Satz: Es gibt mathematisch eindeutige Fragen,
die auch eine eindeutige Antwort haben, wobei diese Antwort aber prinzipiell nicht berechenbar
ist. |
 |
Auf unser Problem übertragen heißt das: Es läßt sich in voller
Strenge mathematisch beweisen, daß es keine Möglichkeit gibt (auf
mathematisch heißt das: keinen endenden Algorithmus), um zu entscheiden, ob ein gegebener Satz von Fliesen die Ebene
vollständig ausfüllen kann (periodisch oder nichtperiodisch; ist egal). |
|  |
Und das, obwohl eine eindeutige Antwort existiert; sie ist entweder
ja oder nein. Damit ist zwar nicht ausgeschlossen, daß man durch Probieren oder Intuition für einen gegebenen
Fliesensatz die Antwort findet; aber grundsätzlich ist das nicht in systematischer Weise für alle beliebigen Sätze
von Fliesen möglich. |
 |
Seit Shechtman's aufregender Entdeckung, hat die Internationale der Materialwissenschaftler
viele Legierungen gefunden (nie einen Elementkristall), die ähnliche Strukturen aufweisen und die als Quasikristalle
bezeichnet werden. Manche dieser Quasikristalle haben Eigenschaften, die sich von denen ihrer kristallinen Brüder mit
derselben Zusammensetzung stark unterscheiden. Sie sind oft härter, schlechter stromleitend und haben Oberflächen,
auf denen (wie beim Teflon) praktisch nichts haftet. |
|
 |
Anwendungen dafür gibt es noch nicht. Die antihaft-beschichtete
Bratpfanne, bei der die Schicht auch nicht schnell wieder abgeht wäre möglich, aber das Image eines derartigen
Produktes ist von der Teflonpfanne gründlich versaut - hier kommt mal wieder die Psychologie
rein. |
|
 |
Aber was nicht ist, kann noch werden. Das Studium der Quasikristalle hat nicht nur die Materialwissenschaft,
sondern auch die Mathematik befruchtet. Früher oder später wird das Früchte tragen. |
 |
Damit ist aber noch lang nicht alles grundsätzliche über Quasikristalle
gesagt, denn die Geschichte geht weiter. Wer wissen möchte, warum Quasikristalle in einer sechsdimensionalen
Welt richtige Kristalle sind, betätigt den Link "Quasikristalle
II" |
| |
© H. Föll (MaWi 1 Skript)



