Balmer Spektrum: Experiment und Bohrsche Theorie

	Balmer entdeckte 1885, daß auf die drei bereits bekannten Emissionslinien des Wasserstoffs im Sichtbaren (Ha,b,g) noch eine ganze Serie von Linien im Ultravioletten folgte. Das Spektrum sah so aus:
		Balmer erkannte, daß hier ein Bildungsgesetz zugrunde liegen muß, das auch gar nicht schwer empirisch zu ermitteln war. Für die Wellenzahl k der Linien gilt:
		k  =   1 l  =  R · æ ç è 1 22   –  1 n2 ö ÷ ø
		mit l = Wellenlänge, R = Rydbergkonstante = 109677,5810 cm–1 (man konnte schon damals sehr genau messen), und n > 2 ganzzahlig.
	Ein einfaches Bildungsgesetz - aber warum? Und was bestimmt den Zahlenwert der Rydbergkonstanten? Niemand konnte diesen experimentellen Befund nachvollziehen, bis 1913 Bohr sein Modell postulierte.
		Welche Sensation das auslöste, kann man ein bißchen nachvollziehen beim Betrachten der folgenden Tabelle.
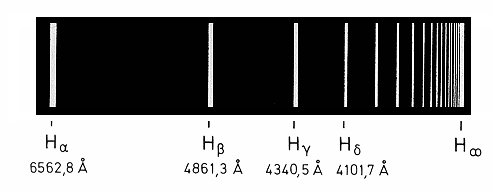
		Linienname n2 (n1 = 2) l beobachtet Å (10–10m) l berechnet Å (10–10m) Ha 3 6562,793 6562,78 Hb 4 4861,327 4861,32 Hg 5 4340,466 4340,45 Hd 6 4101,738 4101,735 He 7 3970,075 3970,074 Hz 8 3888,052 3888,057 Hh 9 3853,387 3835,397 Hd 10 3797,900 3797,910 Hi 11 3770,633 3770,634 Hc 12 3750,154 3750,152 Hl 13 3734,371 3734,372 Hm 14 3721,948 3721,948 Hn 15 3711,973 3711,980

Mit Frame

2.1.2 Fruehe Atommodelle: Bohr und de Broglie

© H. Föll (MaWi 1 Skript)