3.7.4 Summary to: Dielectrics and Optics

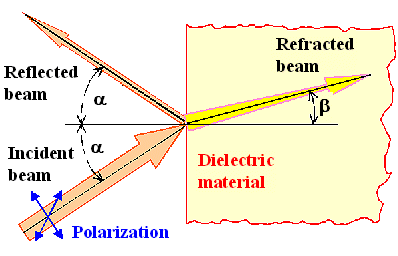
The basic questions one would like to answer with respect to the optical behaviour of materials and with respect to the simple situation as illustrated are:

How large is the fraction R that is reflected? 1 – R then will be going in the material.
How large is the angle b, i.e. how large is the refraction of the material?
How is the light in the material absorped, i.e. how large is the absorption coefficient?

Optical properties and dielectric constant

Of course, we want to know that as a function of the wave length l or the frequency n = c/l, the angle a, and the two basic directions of the polarization (

All the information listed above is contained in the complex index of refraction n* as given Þ

n = (e_r)^1/2

Basic definition of
"normal" index of refraction n

n* = n + i · k

Terms used for complex index of refaction n*
n = real part
k = imaginary part

n*² = (n + ik)² = e' + i · e''

Straight forward definition of n*

Working out the details gives the basic result that

Knowing n = real part allows to answer question 1 and 2 from above via "Fresnel laws" (and "Snellius' law", a much simpler special version).
Knowing k = imaginary part allows to answer question 3 Þ

E_x =	exp –	w · k · x c	· exp[ i · (k_x · x – w · t)]

	Amplitude: Exponential decay with k		"Running" part of the wave

Knowing the dielectric function of a dielectric material (with the imaginary part expressed as conductivity s_DK), we have (simple) optics completely covered!

n²	=	1 2	æ ç è	e'	+	æ è	e' ² +	s_DK² 4e₀²w²	ö ø	½	ö ÷ ø

k²	=	1 2	æ ç è	– e'	+	æ è	e' ² +	s_DK² 4e₀²w²	ö ø	½	ö ÷ ø

If we would look at the tensor properties of e, we would also have crystal optics (= anisotropic behaviour; things like birefringence) covered.

We must, however, dig deeper for e.g. non-linear optics ("red in - green (double frequency) out"), or new disciplines like quantum optics.

Questionaire
Multiple Choice questions to all of 3.7