 |
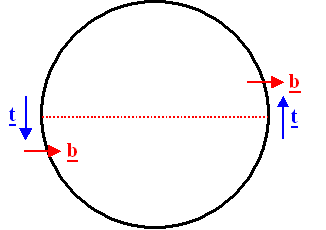
The problem is solved easily by doing one simple thing: Look at the dislocation loop from above |
| |
| | |
|
| | |
|
 |
After assigning a direction of t, it is defined for the whole loop. At the places
where we took the cross-section, it is actually the sign of t that is reversed! The Burgers vector
thus must be "the other way around" if it is to be constant for the local t. |
 |
It is important to realize that we only can be unambiguous if we know that we
are looking at one and the same dislocation. The cross-section by itself does not tell
us that fact; it just as well could show two unconnected single dislocations. In this case we would assign Burgers vectors
with different signs because we "automatically" would take the line direction to be the same. |
| |
© H. Föll (Defects - Script)
![]() Exercise 5.1-1 Sign of Burgers- and Line Vectors
Exercise 5.1-1 Sign of Burgers- and Line Vectors