Solution to Exercise 3.2-1"Crystal Identity"

	The jump rate of a vacancy is identical to that of an atom next to the vacancy. It was given by
		n   =  n0 · exp –   Gm kT    »   n0 · exp –   Hm kT
		The time ta needed so that all the atoms with a vacancy next to them will make one jump thus is
		ta  =  1 n  =   1  n0  · exp  Hm kT
	After that time ta, the fraction of all atoms that had a vacancy a a neighbor, has made one jump.
		If you now wait another ta, a second set of atoms can now make a jump. This second set may include atoms from the first set which simply jump back to their old position, but we ignore this effect for a rough estimate.
		If all atoms of the crystal are supposed to make one jump, you have to wait for a time tc that is a defined multiple of ta. It is simply
		tc  =  m · ta  =  ta cV
		Because the multiplier m is of course the inverse of the vacancy concentration cV = exp – (HF)/kT)
	tc is the quantity we we are looking for, it is
		tc  =  1  n0  · exp  Hm kT   · exp   HF kT   =   1  n0  ·  exp  Hm  +  HF kT   =   1  n0  ·  exp  HSD kT
		With HSD = enthalpy of self diffusion.
	We may replace 1/n0 by 1/n0 = g · a2/ DSD and use the diffusion coefficient for self-diffusion to obtain values for specific materials, but lets just look at what we get in a very simple approximation with n0 = 1013 Hz
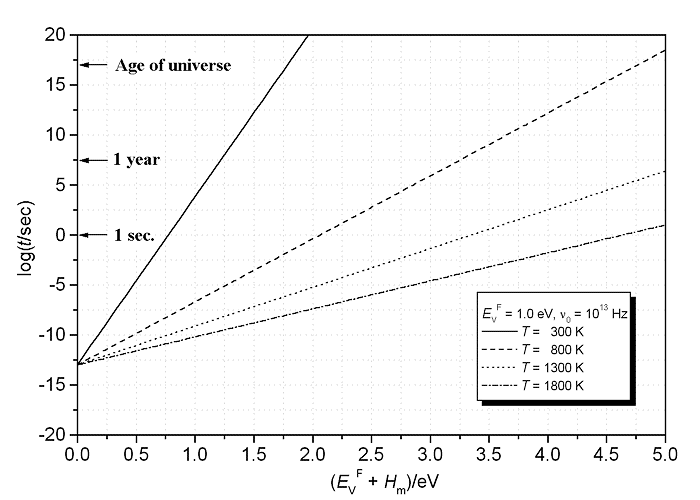
	Shown is tc on a (rather far-reaching) log scale versus Hm + HF = HSD, i.e. the self-diffusion enthalpy HSD, with the temperature as a parameter.
		For Hm + HF = 0, tc is 10–13 s - as it should be.
		For sensible values. e.g. HSD = 2 eV, you must be very patient at room temperature, but at 800 oC, your crystal has a different identity after 1 second! Take Si, with HSD » 5 eV and a melting point of roughly 1700 K, and again no atom will be where it was after a rather short time.
	Using better values for n0 from the self-diffusion coefficient as stated above, just shifts the whole set of curves a "little bit" on the t - axis and thus tc by the same (logarithmic) amount

With frame

Exercise 3.3-1 Quick Questions

Exercise 3.2-1 Crystal Identity

© H. Föll (Defects - Script)