3.3.2 Essentials to Chapter 3.3 Experimental Approaches to Diffusion Phenomena

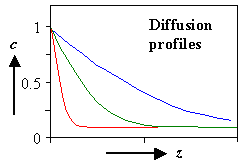
	It's easy in principle: You produce and measure a diffusion profile.
		Put whatever is supposed to diffuse on the crystal surface (make sure you cope properly with the "dirt" or oxide on the surface).
		Let it diffuse at a defined T for a defined time t.
		Measure the diffusion profile "somehow".
		Fit to a solution of Fick's law = one data point for D(T).
		Repeat at different temperatures until you gave enough data points for an (Arrhenius) D(T) plot.
	Use isotopes of the material in question for self-diffusion measurements.
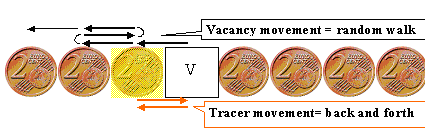
	While the intrinsic point defect serving as diffusion vehicle will do a perfectly random walk, the diffusing atom may not.
		There is a correlation coefficient f linking measured and theoretical diffusion coefficients.
		DSD(T)  =  f1V · DSD(Theo)
		The correlation coefficient f is = 0 for 1dim. diffusion, around 1/2 - 2/3 for 2dim. diffusion (e.g. in the base plane of hexagonal lattices) and around 2/3 - 3/4 for 3dim. diffusion.
	There are many other ways to obtain diffusion data, none fool-proof and all money and/or time expensive.

© H. Föll (Defects - Script)