3.2.4 Essentials to Chapter 3.2 Diffusion Mechanisms

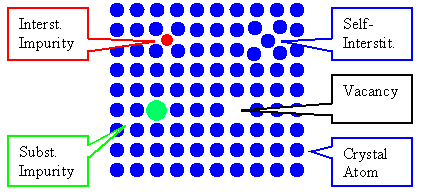
	Considering diffusion in crystals we have exactly three basic cases
		1. An interstitial impurity atom diffuses in the crystal=impurity diffusion.
		2. A substitutional impurity atom diffuses in the crystal=impurity diffusion.
		3. An atom of the crystal diffuses in the crystal=self-diffusion.
	Case 2. and 3. are impossible without diffusion "vehicles", i.e. vacancies (and on occasion self-interstitials).
	Diffusion mechanisms are the atomic mechanisms that are capable of moving atoms. The most important ones are:
		Vacancy mechanism. Accounts for most of cases 2. and 3. from above in simple crystals,
		Direct interstitial mechanisms. Accounts for almost all of case 1.
	Some more complex mechanisms exist (and are of prime importance) in Si (and possibly other semiconductors and somewhat more complex crystals)			Wait and see! And keep an open mind
		"Kick-out" mechanism, impurity and self-diffusion via self-interstitials, ...
	In any case we need the migration enthalpy Hm and entropy Sm of the "jumping" entities to obtain the diffusion coefficient D of the process			Ddir  =  g · a2 · n 0 · exp   S k  ·  exp – Hm kT DSD  =  cV · Dv    =  D*  · exp –   Hm + HF kT
		Typical values are - like always, it seems - in the 1 eV (better: 0.5 eV - 3 eV) and 1 k region, respectively.
		Question to ponder: How long does it take for all atoms of crystal to be somewhere else; i.e. not at the original position? (Exercise 3.2-1)

© H. Föll (Defects - Script)