Solution to Exercise 2.1-2"Do the Math for the Formation Entropy"


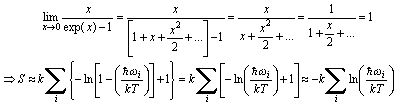
	We start with



	Next we must do the differentiation, i.e. form ¶F/¶T:



	One can go straight ahead, of course. But here comes a little helpful trick: Multiply skillfully by T/T and re-sort; you get



	Now we need to resort to approximations

		First we realize that whenever h ·w/2p << kT, then



		This takes care of the first term.
		The second term needs a somewhat more sophisticated approach. Substituting x for h · w/2p · kT, we can use a simple expansion formula, stop after the second term and re-insert the result. This gives



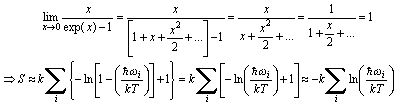	That's as far as one can go. Now use w' for the circle frequencies of the crystal with a vacancy and form S_F = S' – S



		q.e.d.