Figure 7.1:
Euler’s method (two steps). In this simplest (and least accurate) method for integrating
an ODE, the derivative at the starting point of each interval is extrapolated to find the next function value.
As follows from the above remarks, it suffices to consider a first-order ODE for a single-valued function,
|
| \begin{equation*} \label{eq:ODE1} \frac{{\rm d}y}{{\rm d}x} = f(x,y), \end{equation*} | (7.5) |
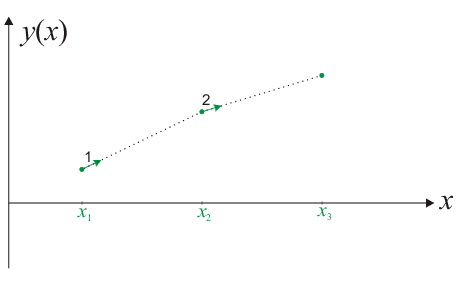
in order to be able to solve all ODE problems. The simplest way to solve such an equation is to use the local slope, which is given by the right-hand side of Eq. (7.5) and which is always known in an initial-value problem, to linearly extrapolate the function and estimate the function value a certain step size away from the starting point. With the new function value at hand, a new slope can be calculated. So the procedure can be repeatedly applied.
Therefore, to proceed from the \(n\)-th position on the \(x\) axis, \(x_n\), to the next position \(x_{n+1} = x_n + h\), one simply has to increment the function value by “step size times slope” (cf. Fig. 7.1):
|
| \begin{equation*} y_{n+1}=y_n+hf(x_n,y_n). \end{equation*} | (7.6) |
Obviously, for this method the step size must be rather small in order to avoid numerical errors.
 |
 |
 |
 |
© J. Carstensen (Comp. Math.)