 |
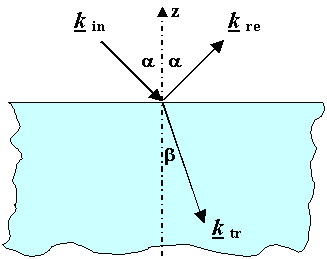
Show that you obtain Itr = Iin –
Iref and Snellius law (sina/sinb =
n) from energy and momentum conservation |
| |
|
|
 |
Solution: |
|
 |
The intensity I of the beams is given by their power (energy /t) which is given by the nunber
of photons/s in the beams: Ein, Ere, Etr. Everythin
always per cm2 but that is not important for what follows. |
|
 |
Energy conservation demands |
| |
| Ein | = |
Ere + Etr |
| | | |
| Etr = |
= |
Ein – Ere |
| | |
|
| Itr = |
|
Iin – Ire |
|
|
 |
Looking at the x-component of the momentum p and considering
that the wavelength in the material is l/n we have |
| |
| |pz, in| | = |
Iin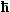 kin · sina kin · sina |
= |
Iin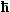 · 2p
· sina · 2p
· sina
l |
| | | |
| | |
| |pz, re| | = |
Ire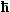 kre · sina kre · sina |
= |
Ire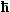 · 2p · sina · 2p · sina
l | | | |
| | |
| | |pz, tr| |
|
Itr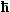 ktr · sinb ktr · sinb |
= |
Itr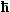 · 2p · sinb · n · 2p · sinb · n
l |
|
|
|
 |
Momentum conservation demands that pz, in + pz,
tr – pz, re = 0, or |
|
|
| Iin sina + Itr sinb
· n – Ire sina |
= | 0 |
|
|
|
 |
Substituting Ire = Iin – Itr leads straight
ot |
| | |
|
© H. Föll (Advanced Materials B, part 1 - script)
![]() Exercise 5.1.1 Derivation of Snellius Law
Exercise 5.1.1 Derivation of Snellius Law ![]() Exercise 5.2.3 Attenuation of Light
Exercise 5.2.3 Attenuation of Light ![]() Exercise 5.2.2 Fresnel Equations and LEDs
Exercise 5.2.2 Fresnel Equations and LEDs ![]() Exercise 5.2.4 Fresnel Equations and Polarization
Exercise 5.2.4 Fresnel Equations and Polarization