5.4.1 Summary to: 5.1 Basic Optics

5.4.1 Summary to: 5.1 Optics

Know your numbers and relations for visible light!

For the propagation of light:
use the wave model
For the generation and disappearance (= absorption) of light:
use the photon model

Snellius law:
n = sina/sinb with a, b the angle of incidence
or propagation, resp.

Wavelengths: l » 400 nm - 800 nm.

l_mat = l₀/n.

Frequency: n» 10 ¹⁵ Hz.

Index of refraction: n = e_r^½ » 1,5 - 2,5

Energy E » 1,8 eV - 3,2 eV.

Dispersion relation: c₀ = n l₀ = 3 · 10⁸ m/s
c_Mat = n l₀/n(l)

Know yout basic equations and terminology

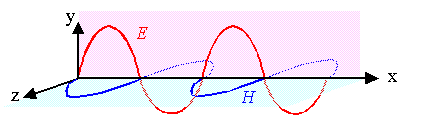Coherent monochromatic plane wave
E and H perpendicular and in phase

E(r,t) H(r,t)	=	E₀ H₀	· exp{i(kr –wt)}

Reflection always with "angle in" = "angle out".

Refraction is the sudden "bending" or "flexing" of light beams at the interface

Diffraction is the continous "bending" of light beams around corners; interference effects.

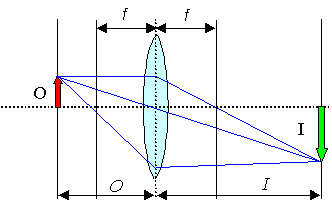
Geometric optics
Key paramters

Focal length f and
numerical aperture NA of lenses, mirrors.

Image formation by simple geometric constration

Various aberrations (spherical. chromatic, astigmatism, coma, ...) limit performance.

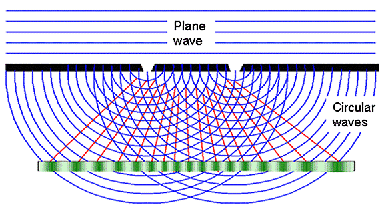
Wave optics
Huygens principle: and interference

Ultimate limit to resolution

d_min	»	l 2NA

Know your basic types of waves:

(Running, coherent, monochromatic) plane wave.

Standing waves = superposition of plane waves.

Incoherent, multichromatic real waves

Relation s between electrical field E, magnetic field H and Poynting vector (energy flow vector) S = E × H

W_elect	=		e₀ · E² 2

W_mag	=		m₀ · H² 2

[W_{elect; magn}]	=		[Ws m^–3]

E₀	=		æ ç è	m_rm₀ e_re₀	ö ÷ ø	½	· H₀	=	Z_w · H₀

<S>	=		E₀H₀ 2	=	E₀² Z_w

This equation links energy flow (easy in photon picture) to field strength in wave picture.

Z_w = wave impedance of the medium.
Z_w(vacuum) = 376,7 W

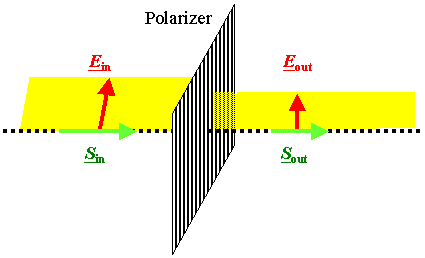
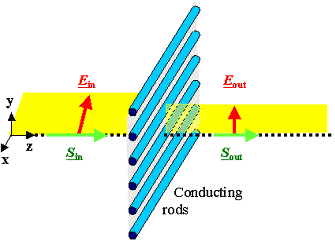
Polarization = key to "advanced" optics.
Simple case: linear polarization.

Plane of polarization contains E-vector and S (k) vector.

Any (coherent) wave is polarized but net polarization of many waves with random polarization is zero!

Light intensity (µ E²) between polarizers at angle a scales with (cosa)².

General case: elliptical polarization; important are the two extremes: linear and circular polarization.

For circular polarizaiton the E-vector rotates on a circle while moving "forward". This results from a superposition of two plane waves with E-vectors ar right angles and a phase difference of p/2.

Technically important (3-dim Cinema; Lab optics)

The task:
Calculate and understand intensities, angles, phases, polarization and attenuation (damping) of the various light beams shown from the materials properties

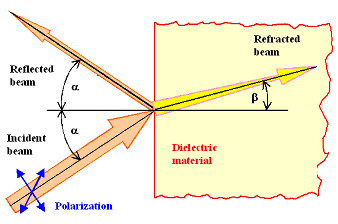
Still assuming a perfectly flat surface

First step: Decompose impinging light into two waves with polarization in he interface plane (TE case) or at right angles (TM case)

Energy conservation yields for the intensities:

I_tr(z = 0)	=	I_in – I_re

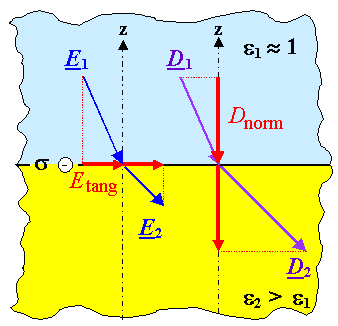
Boundary conditions as shown in the figure involve the "dielectric constant e and thus the so far only relevant material property.

Considering energy (proportional to E²) and momentum (proportional to k²") conservation for the TE and TM case separately yields the Fresnel equations that provide the answers to the questions above

A wealth of insights and relations follow, e.g. or field strength E or intensities I:

E_ref E_in				= –	n – 1 n + 1

	I_ref I_in			=	æ ç è	n – 1 n + 1	ö ÷ ø	2

one consequence as example for the power of these equations: n = 2 means that almost 10 % of the intensity will be reflected, implying that for optical instruments you must provide some "anti-reflection" coating.

Using the complex (and frequency dependent "dielectric constant e(o) = e' + ie'' yields the complex index of refraction

n²	=	1 2	æ ç è	æ è	e' ² + e'' ²	ö ø	½	+ e'	ö ÷ ø

k²	=	1 2	æ ç è	æ è	e' ² + e'' ²	ö ø	½	– e'	ö ÷ ø

n*(o) = n + i k

The imaginary part k describes the attenuation (damping) of the transmitted wave in the material.

Polarization and Material2. How to polarize a light beam

1. Geometry. Use Fresnel equations to produce a polarzed beam under specific angles ("Brewsater angle")

1. Polarization foils = alined conducting rods (of possibly molecular size) "short-circuiting" the electrical field in on direction.

3. "Tensor" materials with optical anisotropy

Theory can an get rather involved; products can be extremely simple and cheap (e.g. circular polarizer in 3-D movie glasses)

Not so perfect materials and properties like specular and diffuse Reflection, transparency, Translucency, Opacity.

Light is scattered at small things in all directions and the scattering of light is the major topic encountered if we look at not-so-perfect materials

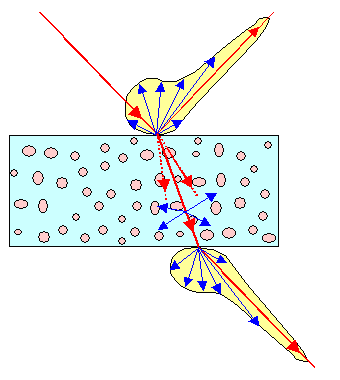
The picture illustrates:
Specular and diffuse reflection at the surface.
Scattering of the transmitted light (running in different directions) at defects or imperfections contained in the material (fat droplets in milk, air bubbles in glass, ...).
Specular and diffuse reflection at the internal surface the light is coming out off. This is described by a (different) polar diagram characterizing this surface.

Scatter mechanism depend on the size l_sca of the scatterer" relative to the wavelength:
l_sca << l: The extreme case would be scattering at single atoms or molecules. Proper nanoparticles also belong into this group. This kind of scattering is called Rayleigh scattering
l_sca >>l: No problem, we covered that already. Just look at any part of the sample by itself.
l_mat » l: Now we have a problem. What will happen in this case is difficult to deal with and no general rules apply. This kind of scattering is called Mie scattering

Generating Light
Two basic cases:

Luminescence:		General name for "cold" light production

Fluorescence:		Light production shortly after energy input. Short life time of excited level (< µs)

Phosphorescence:		Light production long after energy input. Long life time of excited level (> ms)

Light from hot bodies. Planck radiation law applies.
Efficiency tends to be low

Light from "cold" bodies or luminescence

There are many types of cold light production. Of utmost importance is electroluminescence or, to use another word for essentially the same thing, radiant electron - hole recombination in semiconductors.
In yet other words: It's the LED, the light emitting diode..

Specialities

Fresnel Lens
Optical Activity
Faraday effect
Kerr Effect
Pockels Effect

Forget it. The list names some, there are many more.

That's where serious "optics and material" starts. This would need another full lecture course

Light Sources
Hot bodies (tungsten filaments) in light bulbs and plasma discharge in fluorescent tubes

Inefficient light bulbs still dominates when this lecture course started (2010)

LEDs have taken over when this hyperscript was finalized (2019)

Mot included above is the Laser.

You must learn about the Laser somewhere else

Processing light
with, for example, conventional lenses, mirrors and prism, anti-reflection coatings

Even simple light processors like lenses (and the rest from above) might be extremely complex materials engineering products today. Just look at the picture of a (by now (2019) outdated lens for microelectronic lithography-

Polarizers, diffraction gratings and filters add another layer of complexity.

The list goes on, with, e.g. phase shifters and whatever is needed for doing holgraphy or...

Laser "beam forming", modulation, fultr-high speed detection, ...