|
Nernst law is a special answer to the general and important question:
|
| |
How do charged and mobile particles
redistribute themselves in an electrical potential
if there are some restrictions
to the obvious solution
that they all move to one or the other pole of the field? |
|
|
 |
It is the answer to this question that governs not only pn-junctions, but also batteries,
fuel cells, or gas sensors, and, if you like, simply all junctions. |
 |
Let us consider a material that essentially contains mobile carriers of only one kind, i.e. a metal (electrons) , a (doped) semiconductor (electrons or
holes, depending on doping), or a suitable ionic conductor (one kind of mobile ion). |
|
 |
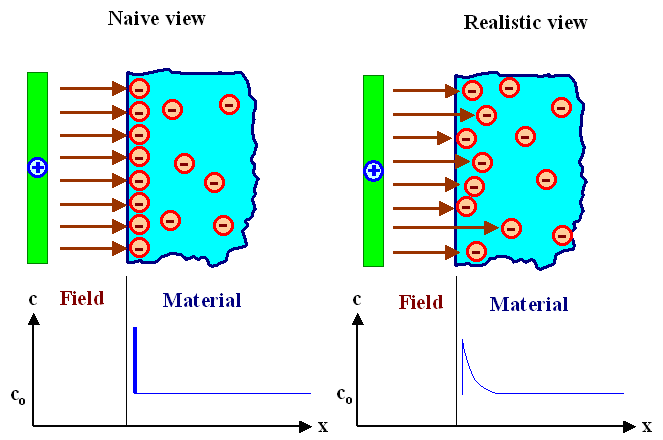
We imagine that we hold a positively charged plate at some (small) distance to the surface
of a material having mobile negative charges (a metal, a suitable ionic conductor, a n-doped semiconductor, ...).
In other words, the positively charged plate and the material are insulated, and no
currents of any kind can flow between the two. However, there will be an electrical field, with field lines starting at
the positive charges on the plate and ending on the negative charges inside the material. We have the following situation: |
| |
|
 |
In a naive (and wrong)
view, enough negatively charged carriers in the material would move to the surface to screen the field completely, i.e.
prevent its penetration into the material. "Enough", to be more precise, means just the right number so that every
field line originating from some charge in the positively charged plate ends on a negatively charged carrier inside the
material. |
|
 |
But that would mean that the concentration of carriers at the surface would be
pretty much a d- function, or at least a function with a very steep slope. That does not
seem to be physically sensible. We certainly would expect that the concentration varies smoothly within a certain distance,
and this distance we call Debye length right away. |
|
 |
As you might know, the Debye length is a crucial material parameter not only in all questions
concerning ionic conducitvity (the field of "Ionics"), but whenever the carrier concentration
is not extremely large (i.e. comparable to the concenetration of atoms, i.e in metals). |
 |
We will now derive a simple formula for the Debye length.
We start from the "naive" view given above and consider its ramifications: |
|
 |
If all (necessarily mobile) carriers would pile up at the interface, we would have a large
concentration gradient and Ficks
law would induce a very large particle
current away from the interface, and, since the particles are charged, an electrical
current at the same time! Since this electrical diffusion
current jel, Diff is proportional
to the concentration gradient –grad (c(x)), we have: |
| |
| jel, Diff(x) = – q · D · grad (c(x))
|
|
|
|
 |
With D = diffusion coefficient. Be clear about the fact that whenever you have
a concentration gradient of mobile carriers, you will always have an electrical current by necessity. You may not notice
that current because it might be cancelled by some other current, but it exists nevertheless. |
 |
The electrical field
E(x), that caused the concentration gradient in the first place, however,
will also induce an electrical field current (also
called drift current) jfield(x), obeying Ohms law
in the most simple case, which flows in the opposite direction of the electrical diffusion
current. We have: |
| |
| jfield(x) = q · c · µ ·
E(x) |
|
|
|
 |
With µ
= mobility, q = charge of the particle (usually a multiple of the elementary charge e of either sign);
q · c · µ, of course, is just the conductivity
s |
|
 |
The total electrical current will then be the sum of the electrical field and diffusion current. |
 |
In equilibrium, both electrical currents obviously
must be identical in magnitude and opposite in sign
for every x, leading for one dimension to |
|
|
| q · c(x) · µ · E(x)
= q · D · |
dc(x)
dx |
|
|
 |
Great, but too many unknowns. But, as we know (????), there is a relation between
the diffusion coefficient D and the mobility µ that we can use; it is the Einstein-Smoluchowski relation (the link leads you
to the semiconductor Hyperscript). |
|
|
|
|
 |
We also can substitute the electrical Field E(x)
by – dU(x)/dx, with U(x) = potential (or, if you like, voltage) across
the system. After some reshuffling we obtain |
|
|
| – e |
dU(x)
dx | = |
kT
c(x) |
· |
dc(x)
dx |
= kT · |
d [lnc(x)]
dx |
|
|
|
 |
We used the simple relation that d (lnc(x)) / dx = 1/c(x) ·
dc(x)/dx. This little trick makes clear, why we always find relations between a voltage and the
logarithm of a concentration. |
|
 |
This is a kind of basic property of ionic devices. It results from the difference of the driving
forces for the two opposing currents as noted before: The diffusion current is
proportional to the gradient of the concentration whereas the field current is directly
proportional to the concentration. |
 |
Integrating this simple differential equation once gives |
| |
| U(x) + | kT
e
| · ln c(x) = const. |
|
|
|
 |
Quite interesting: the sum of two functions of x must be constant for any x
and for any functions conceivable; the above sum is obviously a kind of conserved quantity. |
|
 |
That's why we give it a name and call it the electrochemical
potential
Vec (after muliplying with e so we have energy dimensions). While its two factors will be
functions of the coordinates, its total value for any (x,y,z) coordinate in equilibrium is a constant
(the three dimensional generalization is trivial). In other words we have |
| |
| Vec | = |
V(x) + | kT |
· ln c(x) |
|
|
|
 |
with V(x) = e · U(x) = electrostatic potential energy. |
|
 |
The electrochemical potential thus is a real energy like the potential energy or kinetic energy. |
 |
Obviously, in equilibrium (which means that
nowhere in the material do we have a net current flow) the electrochemical
potential must have the same value anywhere in the material. |
|
 |
This reminds us of the Fermi
energy. In fact, the electrochemical potential is nothing but
the Fermi energy and the Fermi distribution in disguise. |
|
 |
However, since we are considering classical particles
here, we get the classical approximation to the Fermi distribution which is, of course, the Boltzmann
distribution for EF or Vec,
respectively, defining the zero point of the energy scale. |
 |
This is easy to see: Just rewriting the equation from above for c(x)
yields |
| |
| c(x) = exp – |
(Vx) – Vec
kT |
|
|
|
 |
What we have is the simple Boltzmann distribution for
classical particles with the energy (Vx) – Velectrochem. |
| | |
|
|
 |
We may thus assume within a very good approximation that the carrier density at
any point is given by the constant volume density c0 of the field free material, plus a rather small space dependent addition c1(x); i.e. |
| |
|
|
 |
Obviously, only c1(x) is important for Poissons equation. |
 |
From Boltzmanns distribution we know that |
| |
c(x)
c0 | = 1 + |
c1(x)
c0
| = exp |
æ
ç
è |
- |
D(energy)
kT
| ö
÷
ø |
= exp |
æ
ç
è |
– |
V(x)
kT
|
ö
÷
ø |
|
|
|
 |
because the difference in energy of a carrier in the field free volume (i.e. where we have
c0) is simply the electrostatic energy associated with the electrical field. |
|
 |
Since we assumed c1 << c0, we may with impunity
express the exponential function as a Taylor series of which we only retain the first term, obtaining:
|
| |
| 1 + |
c1(x)
c0 |
» 1 + |
V(x)
kT |
|
|
 |
This is a simple trick, but important. Feeding the result back into Poissons equation
yields: |
| |
d2 [c1(x)]
dx2 | = |
e2 · c0 · c1(x)
e · e0 · kT |
|
|
 |
For a simple one-dimensional case with a surface at x = 0 we obtain
the final solution |
| |
|
c1(x) = c1(x = 0) · exp – |
x
d |
|
|
 |
The quantity d is the Debye length we were after, it is obviously
given by |
| |
| d = Debye
length = |
æ
ç
è |
e · e0 · kT
e2 · c0 |
ö
÷
ø |
1/2 |
|
|
|
 |
The Debye length is sometimes also called
Debye-Hückel length (which is historically correct and just). |
|
 |
c1(x = 0), of course, is given by the boundary condition, which for our simple case is:
|
| |
| c1 (x = 0) = c0 ·
|
V (x = 0)
kT |
|
|
 |
What is the meaning of the Debye length? Well, generalizing a bit, we look at
the general case of a material having some surplus charge at a definite position somewhere in a material
|
|
 |
Consider for example the phase boundary of a (charged) precipitate, a charged grain boundary
in some crystal, or simply a (point) charge somehow held at a fixed position somewhere
in some material. The treatment would be quite similar to the one-dimensional case given
here. |
 |
What we know now is quite important: |
|
 |
If you are some Debye lengths away from these fixed charges, you will not "see"
them anymore; their effect on the equilibrium carrier distribution then is vanishingly small. |
|
 |
The Debye length resulting in any one of these situations
thus is nothing but the typical distance needed for screening
the surplus charge by the mobile carriers present in the material. |
|
 |
In other words, after you moved about one Debye length away from the surplus charge, its effects
on the mobile charges of the material are no longer felt. |
 |
More about the Debye length can be found in the Hyperscript "Semiconductors". |
| |
|
© H. Föll (Advanced Materials B, part 1 - script)